Maquen Niño G.L.E., Castro Cárdenas, D.M., Paz Sifuentes, F.A., Pérez Herrera, A. (2024). Conocimiento científico sobre la aplicación de la Inteligencia Artificial en el aprendizaje de las matemáticas.

Una revisión bibliométrica. Revista Reflexiones De La Sociedad Y Economía, 1(2), 87-111. https://doi.org/10.62776/rse.v1i2.17

© Los autores. Este artículo es publicado por la Revista Reflexiones de la sociedad y economía de la Universidad Nacional Pedro Ruiz Gallo de Lambayeque, Perú, como acceso abierto bajo los términos de la Licencia Creative Commons Atribución 4.0 Internacional (https://creativecommons.org/licenses/by/4.0/. Esta licencia permite compartir (copiar y redistribuir el material en cualquier medio o formato) y adaptar (remezclar, transformar y construir a partir del material) el contenido para cualquier propósito, incluido el uso comercial.

RESUMEN

Este estudio revisa la producción científica sobre la aplicación de la inteligencia artificial (IA) en el aprendizaje de las matemáticas mediante un análisis bibliométrico. Se busca identificar patrones y tendencias en la literatura existente, evaluando la evolución de las publicaciones, los autores e instituciones más influyentes, y los temas predominantes. La metodología incluyó una búsqueda sistemática en la base de datos SCOPUS, utilizando una ecuación de búsqueda específica sin limitaciones temporales. Se analizaron 251 publicaciones, y se emplearon herramientas como Bibliometrix, VosViewer y Datawrapper para crear mapas científicos de redes semánticas y de coautorías. Los resultados revelan un aumento significativo en las publicaciones desde 2020, con un amplio interés en temas como la personalización del aprendizaje y la tecnología educativa avanzada. Los autores más destacados, como Li C. y Xing W., han sido identificados como líderes en el campo. Las revistas "Lecture Notes in Computer Science" y "CEUR Workshop proceedings" son las más influyentes. Se observó una fuerte colaboración internacional y entre instituciones, especialmente con una destacada participación de instituciones estadounidenses. Las conclusiones subrayan la importancia de la IA en la educación matemática y destacan áreas de crecimiento futuro, como la ética y la competencia digitales. Sin embargo, una limitación notable del estudio es el uso de una sola base de datos, lo que podría sesgar los resultados.

Palabras clave: Inteligencia artificial, educación matemática, análisis bibliométrico, aprendizaje personalizado.

ABSTRACT

This study reviews the scientific production on the application of artificial intelligence (AI) in mathematics learning through a bibliometric analysis. It seeks to identify patterns and trends in the existing literature, evaluating the evolution of publications, the most influential authors and institutions, and the predominant topics. The methodology included a systematic search in the SCOPUS database, using a specific search equation with no temporal limitations. A total of 251 publications were analyzed, and tools such as Bibliometrix, VosViewer and Datawrapper were used to create scientific maps of semantic networks and co-authorships. The results reveal a significant increase in publications since 2020, with widespread interest in topics such as personalization of learning and advanced educational technology. Top authors, such as Li C. and Xing W., have been identified as leaders in the field. The journals “Lecture Notes in Computer Science” and “CEUR Workshop proceedings” are the most influential. Strong international and inter-institutional collaboration was observed, especially with prominent participation from U.S. institutions. The findings underscore the importance of AI in mathematics education and highlight areas of future growth, such as digital ethics and competence. However, a notable limitation of the study is the use of a single database, which could bias the results.

Keywords: Artificial intelligence, mathematics education, bibliometric analysis, personalized learning

INTRODUCCIÓN

La inteligencia artificial (IA) ha transformado numerosos sectores, incluido el educativo. A nivel global, se ha observado un aumento en el interés por integrar la IA en la enseñanza, especialmente en áreas como las matemáticas, donde la tecnología ofrece soluciones innovadoras para mejorar el aprendizaje (Jin et al., 2022). La capacidad de la IA para personalizar la educación y proporcionar retroalimentación en tiempo real ha impulsado su adopción en diversas instituciones educativas (Gao & Jia, 2021).

A medida que las tecnologías avanzan, la IA se ha convertido en una herramienta crucial para abordar desafíos educativos, como la personalización del aprendizaje y la inclusión de estudiantes con diversas necesidades. Esta tendencia ha sido potenciada por la pandemia de COVID-19, que aceleró la digitalización de la educación. La aplicación de la IA en el aprendizaje de las matemáticas se ha destacado por su potencial para mejorar la calidad educativa, facilitando la comprensión de conceptos complejos (Kaushik et al., 2021).

El problema radica en la falta de claridad sobre cómo se está desarrollando la producción científica en este ámbito. A pesar del creciente interés, no se conoce con precisión cuáles son los patrones y tendencias de las investigaciones sobre la aplicación de la IA en el aprendizaje de las matemáticas. Por ello, este estudio plantea la pregunta de investigación: ¿Cuáles son los patrones y tendencias de la producción científica sobre aplicación de la inteligencia artificial en la enseñanza de la Matemática según un análisis bibliométrico de la literatura existente?

La literatura existente sugiere que la integración de la IA en la educación ha sido diversa y amplia. Autores como Opesemowo & Adewuyi (2024) han explorado el uso de la IA para personalizar el aprendizaje, mientras que Li & Zaki (2024) han investigado cómo los recursos digitales mejoran el aprendizaje de las matemáticas. Tian et al. (2021) también han destacado la importancia de la IA en el desarrollo de habilidades matemáticas básicas, mientras que Moral-Sánchez et al. (2024) han analizado el uso de chatbots de IA en la educación.

Además, estudios recientes han mostrado cómo la IA puede ayudar a los docentes a identificar áreas problemáticas para los estudiantes y, en consecuencia, adaptar sus métodos de enseñanza. Esto ha permitido un enfoque más personalizado y eficiente, beneficiando tanto a estudiantes como a educadores. Sin embargo, también se han identificado desafíos, como la falta de formación de los docentes en tecnologías avanzadas y las limitaciones en la accesibilidad de estas herramientas (Qu et al., 2021).

Este estudio es justificado por la necesidad de entender mejor el panorama actual de la investigación en este campo. A través de un análisis bibliométrico, se busca identificar las principales tendencias y patrones, lo que permitirá a los investigadores y educadores comprender mejor el estado actual del conocimiento y los desafíos futuros. La comprensión de estos aspectos es crucial para la planificación de futuras investigaciones y la implementación efectiva de la IA en la educación matemática.

METODOLOGÍA

Se empleó el análisis bibliométrico para investigar el progreso del conocimiento sobre la aplicación de la IA en el aprendizaje de las matemáticas, siguiendo la metodología de Luna Morales (2020). Este enfoque incluye pasos sistemáticos como la formulación de preguntas, selección de bases de datos, creación de una ecuación de búsqueda y análisis de metadatos.

La investigación adoptó un enfoque cuantitativo, exploratorio y descriptivo, con un diseño no experimental de tipo transeccional. Se construyó una ecuación de búsqueda con términos clave: TITLE-ABS-KEY ("artificial intelligence" OR "machine learning" OR "deep learning" OR "generative intelligence") AND TITLE-ABS-KEY ("mathematics education" OR "math learning" OR "math instruction" OR "mathematics teaching"). No se estableció un límite temporal para abarcar todo el desarrollo del tema desde su inicio en la literatura científica hasta el presente. Se utilizó la base de datos SCOPUS, que proporciona una mayor visión multidisciplinaria, identificando 251 publicaciones científicas.

Los datos extraídos de SCOPUS se exportaron en formato CSV y se convirtieron a XLS para su análisis. Los datos tanto sin procesar, como los procesados están disponibles en el siguiente enlace: https://drive.google.com/drive/folders/1gl6xBp9v7_AGGkfNJYqfBwsXM0eDgbu5?usp=sharing. Se generaron visualizaciones de mapas científicos en forma de redes semánticas y de coautorías, utilizando herramientas especializadas como Bibliometrix, VOSViewer y Datawrapper. Bibliometrix es una herramienta desarrollada en R, respaldada por R Core Team y la R Foundation for Statistical Computing (Bibliometrix, 2023). VOSViewer, un software de código abierto permite crear y visualizar redes bibliométricas (VOSViewer, 2023). Datawrapper facilita la creación de gráficos y tablas estadísticas claras y efectivas, esenciales para comunicar información de manera precisa en contextos académicos y profesionales (Müller, 2023).

ANALÍSIS DE DATOS

Además, el acercamiento facto perceptible o empírico de datos se realizó utilizando la herramienta Bibliometrix de R-Studio y en fases, siendo: I) Evaluación de las publicaciones sobre la aplicación de la IA en la enseñanza de la matemática para visualizar el rango de años con mayor dinamismo en la producción científica. II) Análisis de los autores más relevantes de las investigaciones de la aplicación de la IA en la enseñanza de la matemática utilizando el análisis Bibliométrico bajo la Ley De Lotka. III) Representación gráfica de las 10 revistas especializadas en el tema con mayor números de publicaciones bajo la Ley Bradfort para analizar el núcleo de revistas. IV) Análisis de niveles de colaboración entre autores, instituciones y países en el ámbito de la investigación. V) Análisis de las instituciones financiadoras de los estudios relacionados con la investigación. VI) Niveles de desarrollo semántico alrededor del fenómeno de estudios. VII) Identificación de temas motores, básicos, nichos y emergentes del fenómeno de estudio. VIII) Evaluación espectroscópica (raíces históricas del tema del año de la referencia citada).

RESULTADOS

En esta sección presentaremos la interpretación o derivaciones de cada una de las figuras y tablas obtenidas del consolidado bibliométrico referente a la aplicación de la IA en la enseñanza de la Matemática desde que se empieza a publicar en Scopus, base consultada al respecto, siguiendo como derrotero la siguiente pregunta central de investigación: ¿cuáles son los patrones y tendencias de la producción científica sobre aplicación de la Inteligencia Artificial en la enseñanza de la Matemática según un análisis bibliométrico de la literatura existente?

A partir de la Figura 1 y teniendo en cuenta la interrogante: ¿cuál ha sido la evolución de las publicaciones sobre la aplicación de la IA en el aprendizaje de las matemáticas?, se puede observar la evolución en las publicaciones científicas sobre la aplicación de la IA en el aprendizaje de las matemáticas.

Antes de 2010, el número de publicaciones sobre este tema era muy bajo, con menos de cinco artículos anuales. Esto indica una baja inserción de la IA en el ámbito educativo y un interés incipiente en su aplicación en la educación matemática; en general, fue un periodo de escasa producción científica. Entre 2010 y 2015, el número de publicaciones comenzó a aumentar lentamente, alcanzando aproximadamente entre 10 a 15 artículos anuales hacia el final de este periodo. Este crecimiento moderado refleja un interés creciente y la exploración inicial de las aplicaciones de la IA en la enseñanza de la matemática.

Tabla 1

Principales indicadores bibliométricos de la colección de metadatos

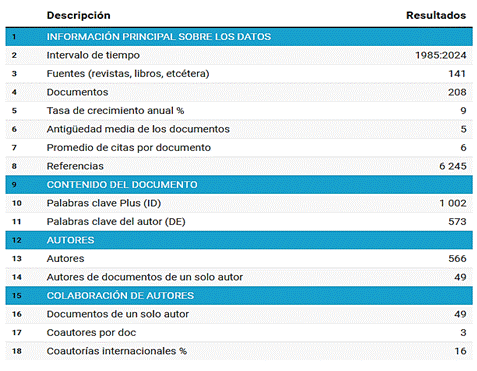
Interfaz de usuario gráfica, Aplicación Descripción generada automáticamente

Nota: Reporte Bibliometrix procesado en Datawrapper.

Figura 1

Evolución de las publicaciones

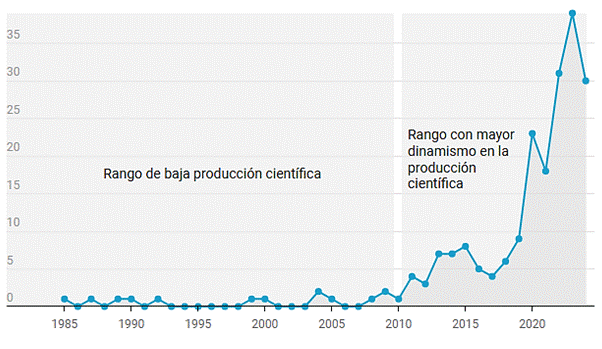
Interfaz de usuario gráfica, Aplicación Descripción generada automáticamente

Nota: La figura muestra un aumento notable en la producción científica a partir del 2010.

Entre 2016 y 2019 hubo una disminución en el número de publicaciones, que osciló entre 4 y 9 por año. Sin embargo, a partir de 2020, el número de publicaciones aumentó considerablemente, alcanzando entre 10 y 40 artículos anuales. Este auge puede estar relacionado con la creciente digitalización de la educación impulsada por la pandemia de COVID-19 y la necesidad de soluciones educativas innovadoras.

Esta tendencia sugiere que el interés y la investigación de la aplicación de la IA en el aprendizaje de las matemáticas está en su punto más alto, reflejando una consolidación del campo y un reconocimiento de su importancia en la educación moderna.

Tabla 2

Principales autores

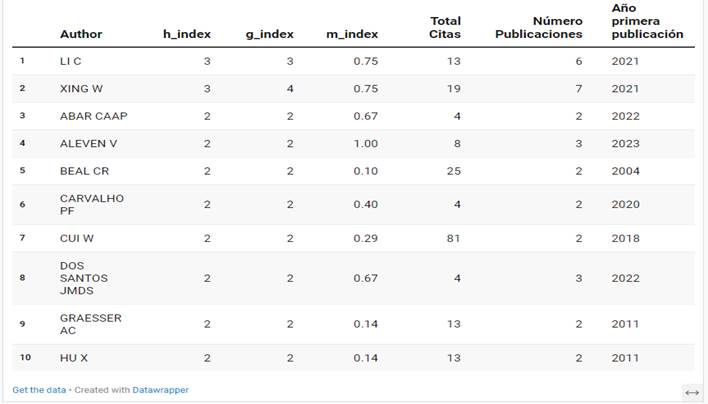
Tabla

Descripción generada automáticamente

Nota: Reporte Bibliometrix procesado en Datawrapper.

En la dirección de la pregunta: ¿quiénes son los autores más relevantes en el tema de la aplicación de la IA en la enseñanza de la matemática?, analizamos la tabla 2, que muestra que los autores Li C. y Xing W. destacan como los más influyentes y productivos en esta área. Sus elevados índices h y el considerable número de citas indican un impacto significativo y una alta calidad en sus investigaciones.

Por otra parte, Abar Caap, Aleven V, Beal CR y Carvalho PF también muestran una actividad destacada, aunque en menor medida en comparación con Li C. y Xing W. Estos autores, a pesar de tener un menor número de publicaciones y citas, contribuyen de manera notable al avance de este campo de estudio. En conjunto, la información obtenida permite identificar a los líderes de investigación en este ámbito y resalta la importancia de sus contribuciones en el desarrollo de la inteligencia artificial aplicada a la educación matemática.

Li C., con un total de 6 publicaciones, índice h igual a 3, índice m 0.75, índice g 3 y un acumulado de 13 citas, se posiciona como uno de los autores más activos y destacados en el campo, lo que indica una fuerte influencia en el área de investigación.

Seguidamente, se ubica Xing W. Con 7 publicaciones, índice h 3, índice m 0.75, índice g 4 y 19 citas, destaca como autor prominente, mostrando un buen equilibrio entre productividad y el impacto de sus publicaciones, evidenciado por sus índices bibliométricos.

Otro autor que demuestra una actividad constante y un impacto considerable en el campo de estudio, reflejado en sus índices y número de citas, es Abar Caap, 2 publicaciones, índice h 2, índice m 0.67, índice g 2 y 4 citas.

Aleven V., al haber publicado 3 documentos, tener índice h igual a 2, índice m 1, índice g 2 y haber logrado 8 citas, se podría decir que contribuye notablemente al área de investigación. Asimismo, Beal C.R. es un autor relevante, aunque con un menor número de publicaciones y citas en comparación con los otros autores mencionados, con 2 publicaciones, índice h 2, índice m 0.10, índice g 2, y 25 citas.

Por otro lado, la tabla 3 presenta los datos obtenidos mediante el análisis bibliométrico aplicado bajo la Ley de Lotka. Esta ley establece una relación inversa entre el número de autores y el número de publicaciones que realizan (Lotka, 1926). Específicamente, se observa que muy pocos autores producen varios artículos, mientras que la mayoría contribuye con un menor número. Como muestra la tabla 3, los autores con una sola publicación son el grupo más numeroso, los que tienen 2 publicaciones son ya un grupo significativamente menor, y van disminuyendo aún más a medida que aumenta el número de publicaciones, lo que es consistente con lo que la Ley de Lotka predice.

Tabla 3

Ley de Lotka

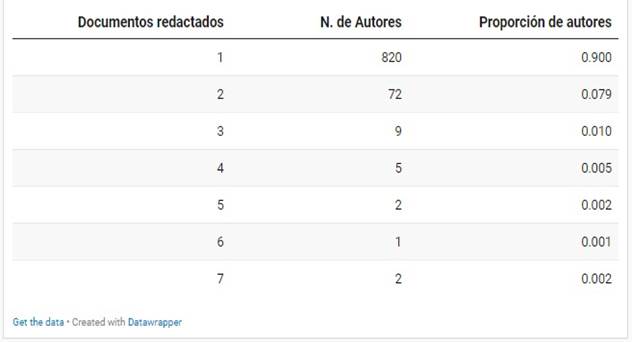
Tabla

Descripción generada automáticamente

Nota: Reporte Bibliometrix procesado en Datawrapper.

Figura 2

Ley de Lotka

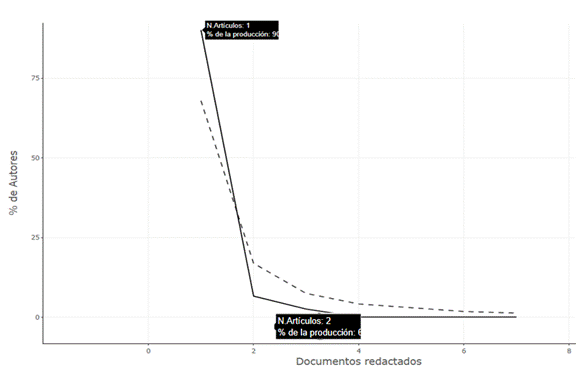
Nota: La figura muestra que la mayoría de los autores publicaron un solo documento, representando el 90% de la producción total.

La figura 2 es una representación gráfica de los datos de la Ley de Lotka, procesados con Biblometrix y visualizados en Datawrapper. Esta gráfica muestra de manera clara la relación descrita anteriormente, visualizando la distribución de autores por el número de publicaciones. En el eje X (número de publicaciones) se presenta el número de artículos publicados por los autores; en el eje Y (número de autores), la cantidad de autores correspondiente a cada número de publicaciones. Entonces, se puede observar que:

· La curva descendente confirma que la mayoría de los autores publica solo un artículo.

· A medida que aumenta el número de publicaciones, la cantidad de autores disminuye drásticamente.

· La pendiente de la curva es empinada al inicio y se suaviza hacia la derecha, lo que es característico de la distribución descrita por la Ley de Lotka.

Tabla 4

Principales 10 revistas especializadas (Zona 1 Ley de Bradford)

Tabla

Descripción generada automáticamente

Nota: Reporte Bibliometrix procesado en Datawrapper.

Figura 3

Ley de Bradford

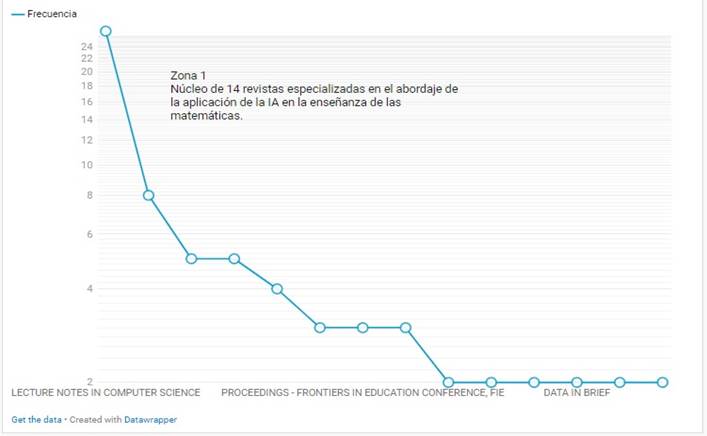
Gráfico, Gráfico de líneas

Descripción generada automáticamente

Nota: La figura muestra el núcleo de 14 revistas especializadas en la aplicación de IA en la enseñanza de matemáticas.

En la tabla 4, se enumeran las 10 revistas más importantes relacionadas con el tema de investigación, según el análisis bibliométrico. Estas revistas son cruciales porque publican la mayor cantidad de artículos relevantes en el área de estudio. Se desprende de la observación de esta tabla, que las revistas que más han publicado sobre aplicación de la inteligencia artificial en el aprendizaje de las matemáticas y que se identifican como las más importantes y centrales en el campo debido a su alta frecuencia de publicaciones son: Lecture Notes in Computer Science con una frecuencia de 27, seguida de CEUR Workshop proceedings, con una frecuencia de 8, Computers & Education, frecuencia 6, British Journal of Educational Technology y Journal of Computer Assisted Learning con frecuencia 5, Educational Technology Research and Development y International Journal of Artificial Intelligence in Education con frecuencia 4, Journal of Educational Computing Research e Interactive Learning Environments frecuencia 3 y Journal of Educational Technology & Society con frecuencia 3.

Este dato es corroborado con la Figura 3 que muestra la Ley de Bradford aplicada al tema (Brookes, 1985). La gráfica ilustra que las revistas Lecture Notes in Computer Science y CEUR Workshop proceedings se ubican en la zona 1 y en la parte más elevada, es decir, en el núcleo de las revistas especializadas en el abordaje del tema.

La figura 3 muestra que las revistas en la zona 1 son pocas, pero contienen la mayoría de los artículos publicados sobre el tema, mientras que las zonas 2 y 3 contienen más revistas, pero con menos artículos cada una. Este patrón es consistente con la Ley de Bradford, que describe cómo una pequeña cantidad de revistas concentra la mayor parte de la literatura científica en un campo específico. La Ley de Bradford muestra que estas revistas se ubican en la zona 1 y en la parte más elevada, es decir, en el núcleo de las 62 revistas especializadas en el abordaje de la aplicación de la inteligencia artificial en el aprendizaje de las matemáticas.

En resumen, las revistas más importantes relacionadas con el tema, basadas en la frecuencia de publicaciones, son Lecture Notes in Computer Science y CEUR Workshop proceedings, seguidas por otras revistas listadas en la tabla 4. Estas revistas se ubican en la zona 1, según la Ley de Bradford, lo que significa que son esenciales para la difusión del conocimiento en este campo. La figura 3 respalda esta conclusión, mostrando cómo estas revistas ocupan una posición central en la distribución de artículos.

Figura 4

Relación autores, filiaciones y países

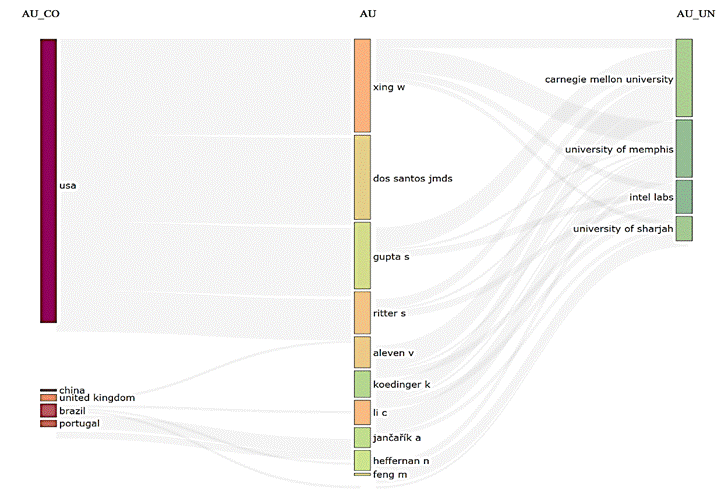
Escala de tiempo Descripción generada automáticamente

Nota: La figura visualiza las conexiones entre autores, sus afiliaciones institucionales y países de origen en el ámbito de investigación.

Se establece la interrogante: ¿qué niveles de colaboración han tenido los autores, instituciones, países, etc.?

La figura 4 muestra un alto nivel de colaboración entre autores, instituciones y países en el ámbito de la investigación. La mayoría de los autores destacados pertenecen a Estados Unidos, indicando una significativa producción académica y colaboración interna. Entre los autores, Xing, W. (Carnegie Mellon University), Dos Santos, JMDS (University of Memphis), Gupta, S. (Intel Labs), y Ritter, S. (University of Sharjah) destacan por su afiliación con instituciones reconocidas, reflejando tanto la colaboración académica como la conexión con la industria.

Carnegie Mellon University, University of Memphis, Intel Labs y University of Sharjah son ejemplos de instituciones que participan activamente en esta red colaborativa. La presencia de autores afiliados a instituciones fuera de Estados Unidos, como la University of Sharjah, subraya la colaboración internacional. Además, la relación entre Intel Labs y autores académicos ilustra una notable interacción entre el sector industrial y el académico.

Figura 5

Instituciones financiadoras de investigaciones

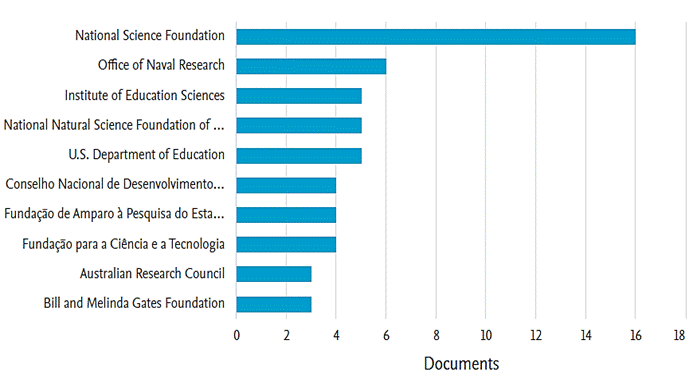
Gráfico, Gráfico de barras Descripción generada automáticamente

Nota: La figura destaca las principales instituciones financiadoras, con la National Science Foundation liderando en cantidad de documentos financiados.

De acuerdo con la interrogante: ¿qué instituciones se han comportado como financiadoras de los estudios relacionados con el fenómeno?, en la figura 5 se observa a las instituciones que han actuado como financiadoras de los estudios relacionados con el fenómeno, son diversas y de gran renombre. La National Science Foundation (NSF) se destaca como la principal financiadora, apoyando el mayor número de documentos. Le sigue Office of Naval Research (ONR), que también ha contribuido significativamente al financiamiento de investigaciones. El Institute of Education Sciences (IES) y la National Natural Science Foundation of China han financiado también un número considerable de estudios.

Del mismo modo, el U.S. Department of Education y el Conselho Nacional de Desenvolvimento Científico e a Tecnológico (CNPq) han sido importantes patrocinadores, junto con la Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) y la Fundação para a Ciência e a Tecnologia (FCT). Otras instituciones relevantes incluyen el Australian Research Council (ARC) y la Bill and Melinda Gates Foundation, aunque esta última ha financiado un menor número de documentos en comparación con las demás.

Figura 6

Análisis factorial

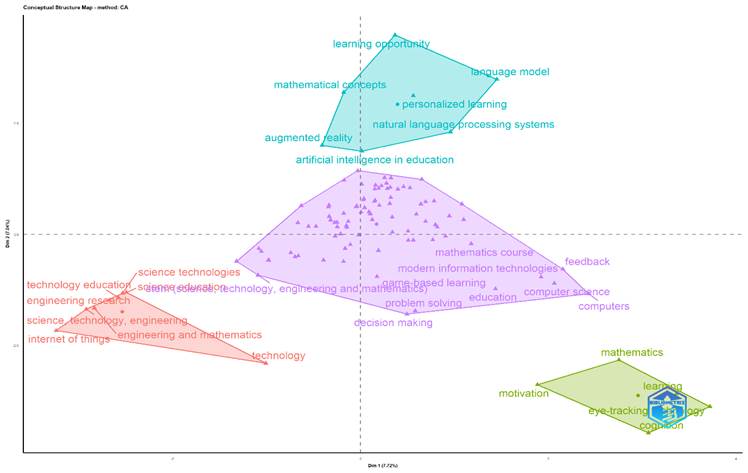
Gráfico Descripción generada automáticamente

Nota: El mapa muestra agrupaciones temáticas en la intersección de inteligencia artificial, educación y tecnología, destacando conceptos como aprendizaje personalizado, realidad aumentada y procesamiento de lenguaje natural.

De acuerdo con la pregunta: ¿cuál es el desarrollo semántico alrededor del fenómeno en estudio?, en la figura 6 se visualiza el mapa factorial que muestra las relaciones semánticas de los temas relacionados a la aplicación de la inteligencia artificial en el aprendizaje de la matemática, presentando 4 grupos de áreas temáticas.

La agrupación verde se centra en temas relacionados con procesos educativos como la motivación en el aprendizaje de las matemáticas, el uso de tecnología como el seguimiento ocular (eye-tracking) para mejorar el aprendizaje de las matemáticas, y la "cognición" para entender cómo los estudiantes procesan la información.

En la agrupación celeste, los temas giran en torno a la aplicación de la inteligencia artificial en la educación, incluyendo el uso de realidad aumentada, modelos de lenguaje y sistemas de procesamiento de lenguaje natural. Asimismo, los temas "aprendizaje personalizado" y "oportunidad de aprendizaje" sugieren un énfasis en la personalización del aprendizaje y la creación de nuevas oportunidades educativas mediante el uso de tecnologías avanzadas.

Por otro lado, la agrupación morada aborda la integración de metodologías innovadoras y tecnologías de la información en el aprendizaje de las matemáticas. Temas como “resolución de problemas", “toma de decisiones” y "aprendizaje basado en juego" indican un interés en metodologías innovadoras, el tema STEM indica la intersección entre ciencia, tecnología, ingeniería y matemáticas, y temas como "Ciencias de la computación" y "tecnologías de la información modernas" destacan la relación entre la informática y la actividad educativa.

Finalmente, la agrupación roja indica un interés en cómo diferentes disciplinas científicas se integran y se aplican en la educación, incluyendo temas como tecnologías científicas, educación científica, educación tecnológica, investigación en ingeniería, ciencia tecnología ingeniería e ingeniería y matemáticas.

En conclusión, el mapa factorial abarca una diversidad de temas que van desde la comprensión de procesos educativos, como la motivación y la cognición, hasta la implementación de metodologías innovadoras y tecnologías de la información modernas en la enseñanza. Se observa una fuerte tendencia hacia la personalización del aprendizaje y la creación de nuevas oportunidades educativas mediante la inteligencia artificial, así como una integración significativa de disciplinas STEM, lo que subraya la importancia de un enfoque multidisciplinario para aplicar la inteligencia artificial en el aprendizaje de las matemáticas.

Figura 7

Mapa temático estructural

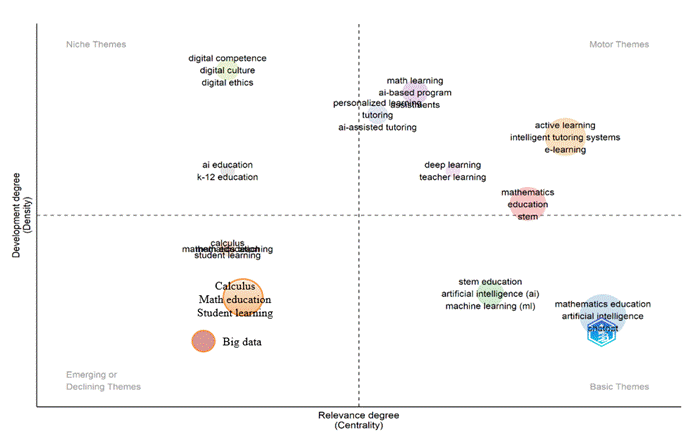
Nota: El mapa clasifica temas de investigación según su relevancia y desarrollo, destacando áreas emergentes como "big data" y temas motores como "aprendizaje activo" y "sistemas de tutoría inteligente".

En relación con la pregunta: ¿cuáles son los temas motores en torno al fenómeno en estudio, perspectivas, nichos y temas emergentes?, en la figura 7 se visualiza un mapa temático que muestra los temas relacionados con el fenómeno de estudio, clasificados según su centralidad y densidad correspondientes a la relevancia y grado de desarrollo, respectivamente.

Los “temas motores”, al tener alta centralidad y densidad, son los temas relevantes y comúnmente desarrollados en el campo de estudio. Se destacan cuatro grandes grupos: el primero, relacionado con el aprendizaje en línea, los sistemas inteligentes de tutoría y el aprendizaje activo, aborda el soporte tecnológico para la enseñanza. El segundo grupo, enfocado en la educación, matemáticas y STEM, abarca el contenido curricular. El tercer grupo incluye temas como asistencia, aprendizaje de matemáticas y programas basados en inteligencia artificial, y se centra en la integración de la IA como herramienta didáctica para la construcción del aprendizaje. Por último, un grupo relacionado con el aprendizaje personalizado, la tutoría y la tutoría asistida por inteligencia artificial se encuentra dentro del cuadrante de “temas motores”, muy cercano al de “temas nicho”, lo que sugiere una leve disminución en la relevancia de estos temas.

Por otro lado, los “temas nicho” tienen alta densidad, pero baja centralidad, lo que significa que están altamente desarrollados, pero son menos centrales en el campo. Se encuentran dos grandes grupos: el primero, relacionado con la competencia digital, cultura digital y ética digital, abarca las características y requisitos necesarios para un proceso educativo mediado por computadora. El segundo grupo se centra en la educación con inteligencia artificial y la educación K-12, que refiere a la aplicación de la inteligencia artificial en distintos niveles educativos: inicial, primario y secundario.

Si se analiza el cuadrante de “temas básicos”, teniendo en cuenta que tienen alta centralidad y baja densidad, es decir, son relevantes pero menos desarrollados, contiene dos grandes grupos: el grupo relacionado con educación matemática, inteligencia artificial y chatgpt, que refiere al uso de programas informáticos que simulan a un experto humano para entablar una conversación con el usuario final, utilizando técnicas conversacionales basadas en inteligencia artificial, y el grupo relacionado con educación STEM, inteligencia artificial (IA) y machine learning que se refiere al uso de algoritmos de inteligencia artificial para que el sistema informático sea capaz de aprender de los datos, encontrando patrones que le permitan obtener conclusiones, imitando el modo en que aprenden los humanos.

Por último, el cuadrante de los “temas emergentes” que tienen baja densidad y centralidad, está conformado por dos grupos: el grupo de cálculo, educación matemática y aprendizaje del estudiante y el grupo unitario Big Data, que refieren a temas en declive con poco interés o relevancia para los investigadores.

En conclusión, los temas motores que son altamente desarrollados y relevantes se enfocan en la tecnología de soporte educativo, contenido curricular y la personalización del aprendizaje. Los temas nicho que son altamente desarrollados y menos relevantes se enfocan en la competencia y ética digital, así como la educación en diferentes niveles educativos. Por otro lado, los temas básicos conformados por la educación matemática, inteligencia artificial, chatgpt y machine learning son temas relevantes, pero requieren mayor desarrollo. Por último, están los temas emergentes como el cálculo y Big Data.

Figura 8

Espectroscopía del año de la referencia citada (raíces históricas del tema)

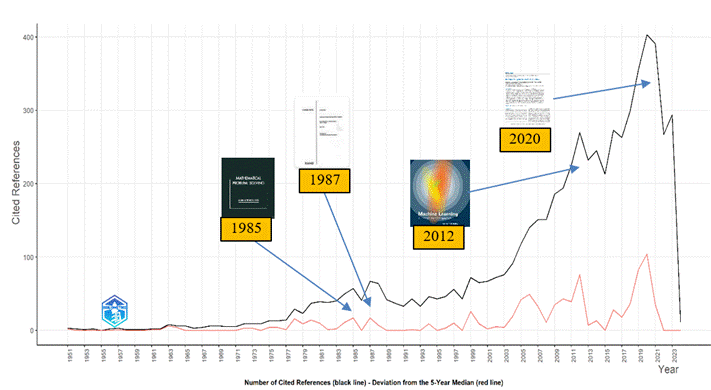
Nota: La figura muestra las referencias clave en el desarrollo del tema, destacando obras de 1985, 1987, 2012 y 2020 que marcaron picos significativos en citas.

En la evolución del conocimiento científico sobre la aplicación de la inteligencia artificial en el aprendizaje de las matemáticas, varios estudios han sido esenciales (ver figura 8). Estos estudios han contribuido significativamente a la comprensión y desarrollo teórico del concepto. En esta investigación se empleó el método de espectroscopía del año de la referencia citada para examinar la evolución histórica de los conceptos relacionados con la aplicación de la IA en la enseñanza de la matemática. Este enfoque cuantitativo permite identificar las raíces históricas de los campos de estudio y medir su influencia en la investigación contemporánea. Se basa en el análisis de la frecuencia con la que se citan referencias en publicaciones dentro de un área de estudio específica, en relación con los años de publicación de esas referencias. Los orígenes se revelan a través de picos notables, que generalmente resultan de publicaciones individuales que se citan con frecuencia.

En el año 1985, Alan H. Schoenfeld publicó Mathematical Problem Solving. Este libro considera posible el análisis de la matemática a partir de cuatro categorías: recursos, heurísticas, control y sistemas de creencias (Schoenfeld, 2014). En la categoría de control, Schoenfeld describe los esquemas de codificación de protocolos aplicados tanto en la inteligencia artificial como en la educación matemática, los cuales están diseñados para producir registros objetivos de las secuencias de acciones que los individuos llevan a cabo al resolver problemas. Asimismo, deja entre ver cómo la IA permite una mejor administración y toma de decisiones a través de un programa que simule la conducta de un protocolo, conceptos esenciales y actualmente vigentes, ya que manifiestan la interacción de la IA y el aprendizaje matemático.

El artículo Learning Problem-Solving Skills in Algebra de McArthur, D., Stasz, C., y Hotta describe un tutor inteligente cuyo objetivo es desarrollar un sistema de tutoría por computadora que emule a un tutor humano experto. Destaca las capacidades de estos tutores como oportunidades para el aprendizaje del álgebra básica y cómo pueden ayudar a desarrollar habilidades, conocimientos y razonamientos orientados a objetivos (McArthur et al., 1987). El artículo subraya la instrucción asistida por computadora (CAI) y presenta tres aspectos cruciales en su sistema tutorial: el conocimiento de la materia, el conocimiento del estudiante y el conocimiento de técnicas pedagógicas que faciliten el aprendizaje del álgebra. Este artículo, de gran relevancia, es uno de los pioneros en la aplicación e interrelación de la IA y el aprendizaje de las matemáticas, siendo fundamental para la conceptualización y la comprensión de la IA y su aplicabilidad en el aprendizaje de la matemática.

En 2012, Machine Learning. A Probabilistic Perspective de Kevin P. Murphy‘ resalta cómo el aprendizaje automático busca desarrollar métodos y patrones para identificar datos de forma automatizada, permitiendo predecir resultados futuros. Este libro ofrece una introducción detallada al campo, con ejemplos de aplicaciones en biología molecular, procesamiento de textos, visión por computadora y robótica. Está dirigido a estudiantes universitarios avanzados y principiantes de posgrado en informática, estadística, ingeniería eléctrica, econometría u otras disciplinas con conocimientos matemáticos adecuados, incluyendo cálculo multivariado, probabilidad, álgebra lineal y programación. Enfatiza un enfoque basado en modelos para el aprendizaje automático, proporcionando un marco sistemático para abordar problemas inferenciales y desarrollar soluciones robustas, contribuyendo con aspectos teóricos y desarrollo de sistemas de automatización (Murphy, 2012).

En 2020, Chen, L., Chen, P., y Lin, Z., publicaron el artículo "Artificial Intelligence in Education: A Review". En este trabajo, se examina cómo las inteligencias artifiales está transformando la educación, con aplicaciones como tutores inteligentes que personalizan la enseñanza, sistemas automatizados de evaluación que proporcionan retroalimentación inmediata y plataformas de aprendizaje adaptativo que ajustan el contenido según el progreso del estudiante(Chen et al., 2020). También se consideran los desafíos y las cuestiones éticas relacionadas con la implementación de la IA en la educación, como la privacidad de los datos y la equidad en el acceso a la tecnología. Además, se analiza el futuro y el potencial de la IA para mejorar la educación, destacando la importancia de la investigación continua y la colaboración entre educadores, tecnólogos y legisladores para maximizar los beneficios y mitigar los riesgos. Este artículo es valioso para comprender la evolución de la IA en el aprendizaje de las matemáticas y las amplias posibilidades de aprendizaje que puede ofrecer.

DISCUSIÓN DE RESULTADOS

La evolución de las publicaciones revela un interés creciente en la aplicación de la inteligencia artificial en la enseñanza de la matemática, especialmente desde el año 2020. Este interés se refleja también en el artículo de Kaushik et al. (2021), que destaca cómo la inteligencia artificial está siendo adoptada cada vez más en el ámbito educativo para mejorar la enseñanza y el aprendizaje de la matemática. Esta convergencia sugiere que las investigaciones reconocen la importancia de la IA en la educación, impulsada por la necesidad de soluciones innovadoras en contextos como la pandemia de COVID-19.

En cuanto a los autores más relevantes, se identifica a C. Li & Xing (2022) como los más influyentes en este campo. Esto es consistente con las conclusiones de Opesemowo & Adewuyi (2024), quienes también destacan a estos autores por su contribución significativa al desarrollo de sistemas de tutoría inteligente y métodos de aprendizaje personalizado. Esta coincidencia subraya la centralidad de estos investigadores en la promoción de la IA en la educación matemática.

El análisis de las principales revistas muestra que "Lecture Notes in Computer Science" y "CEUR Workshop proceedings" son las más importantes, publicando la mayoría de los artículos relevantes en este campo. Esto se alinea con la Ley de Bradford y con el trabajo de Qu et al. (2021), que enfatiza la concentración de publicaciones clave en unas pocas revistas especializadas, lo que facilita la difusión del conocimiento en el área de la inteligencia artificial aplicada a la educación matemática.

En cuanto a la colaboración entre instituciones, esta revela una significativa interacción entre autores e instituciones de Estados Unidos y otras partes del mundo. Esto se refleja también en la investigación de Gao & Jia (2021), que resalta la colaboración internacional y el intercambio de conocimientos como factores clave para el avance de la inteligencia artificial en la educación. La colaboración entre universidades y la industria, como Intel Labs y Carnegie Mellon University, subraya la sinergia entre investigación académica y aplicación práctica.

El desarrollo semántico de la investigación en este campo muestra una diversificación en las áreas temáticas, con un enfoque en la personalización del aprendizaje y el uso de tecnologías avanzadas. Esto es respaldado por el estudio de X. Li & Zaki (2024), que analiza el impacto de los recursos digitales y las metodologías innovadoras en la enseñanza de la matemática. Estos estudios coinciden en la importancia de adaptar la enseñanza a las necesidades individuales de los estudiantes mediante la IA, promoviendo un aprendizaje más efectivo y personalizado.

También se identifica temas motores y emergentes en la investigación sobre la aplicación de la IA en la enseñanza de la matemática. Los sistemas de tutoría inteligente y el aprendizaje personalizado se destacan como áreas de desarrollo clave, lo que coincide con el trabajo de Chen et al. (2020), que subraya la relevancia de estos sistemas para mejorar la educación. Por otro lado, temas como la ética y las competencias digitales, aunque desarrollados, no son tan centrales en el campo, lo que indica una posible área de crecimiento para futuras investigaciones (Murphy, 2012).

La investigación ofrece una visión comprensiva y actualizada de las tendencias y patrones en la aplicación de la inteligencia artificial en la enseñanza de la matemática. Este estudio destaca la importancia de la colaboración internacional, la diversificación temática y la personalización del aprendizaje como factores clave para el avance del campo.

DELIMITACIÓN DEL ESTUDIO

Se debe resaltar que la presente investigación solo ha realizado el estudio con la base de datos de Scopus, porque existe un vacío en la metodología para la realización de estudios bibliométricos que contemple la utilización de varias bases de datos. Se sugiere que, para futuras investigaciones, se puedan contemplar el uso de nuevas metodologías que permitan la utilización de diversas bases de datos.

Para una visión más completa y representativa, en futuras investigaciones estamos considerando usar una mayor variedad de fuentes y continuar explorando áreas emergentes. La colaboración interdisciplinaria y la integración de nuevas tecnologías seguirán siendo esenciales para maximizar el impacto de la IA en el aprendizaje de las matemáticas.

CONCLUSIONES

Las conclusiones de esta revisión bibliométrica muestran un notable aumento en las publicaciones sobre la aplicación de la IA en el aprendizaje de las matemáticas, especialmente desde 2020, lo que refleja un interés creciente en esta tecnología educativa. Los autores más influyentes en este campo son Li C. y Xing W., cuyas contribuciones son significativas. Las revistas más destacadas incluyen "Lecture Notes in Computer Science" y "CEUR Workshop proceedings". Se observa una fuerte colaboración institucional, especialmente con instituciones estadounidenses y una creciente colaboración internacional, lo cual es crucial para el desarrollo del campo. El desarrollo semántico del área es variado, enfocándose en la personalización del aprendizaje y la implementación de tecnologías avanzadas. Se destacan temas desde la motivación hasta metodologías innovadoras. Los sistemas de tutoría inteligente y el aprendizaje personalizado son temas motores, mientras que la ética y la competencia digital, aunque menos centrales, representan áreas para futuras investigaciones. Los patrones y tendencias de la producción científica indican un creciente interés y diversificación temática con un enfoque en la integración de la IA en la educación matemática. Se destaca la importancia de la colaboración interdisciplinaria y la adaptación de tecnologías emergentes para mejorar la calidad educativa.

APORTES DE LOS AUTORES (Según taxonomía CRediT)

Gisella Luisa Elena Maquen Niño realizó la conceptualización y la redacción del borrador original, Diana Mercedes Castro Cárdenas estableció la metodología de trabajo y revisión del análisis formal, Freddy Asrael Paz Sifuentes estableció la visualización de gráficos, figuras y tablas y supervisó el cumplimiento de la metodología , Adelmo Pérez Herrera realizó la revisión y edición de los borradores y la supervisión del progreso del proyecto. Todos los autores realizaron el levantamiento de observaciones y dieron su aprobación de la versión final.

CONFLICTO DE INTERESES

Los autores declaran que no existen conflictos de intereses que puedan haber influido en la realización de esta investigación, el análisis de los resultados o la redacción del presente manuscrito.

RESPONSABILIDAD ÉTICA Y LEGAL

Este estudio se llevó a cabo respetando el Código de ética de la Asociación Estadounidense de Psicología (APA). Se trabajó con documentos de archivo y fuentes secundarias, asegurando un manejo ético de la información, el respeto a los derechos de autor, y la adecuada citación de los materiales utilizados. Se ha garantizado que la interpretación de los datos históricos se realiza con rigurosidad y responsabilidad, sin distorsionar el contexto original.

DECLARACIÓN SOBRE EL USO DE INTELIGENCIA ARTIFICIAL - LLM (Large Language Model)

En esta investigación se utilizó el modelo de lenguaje extenso ChatGPT-4 para apoyar la redacción de secciones preliminares del manuscrito y para mejorar la redacción de los textos. Sin embargo, toda la interpretación de resultados, redacción final y conclusiones fueron revisadas y validadas por los autores, quienes asumen la plena responsabilidad sobre el contenido presentado. Los autores son responsables de la veracidad, integridad y precisión de los datos y argumentos presentados. Reconocemos que los modelos de lenguaje pueden contener sesgos o limitaciones inherentes, por lo que todo el contenido fue revisado para asegurar su adecuación a los estándares académicos.

FINANCIAMIENTO

Este estudio fue financiado íntegramente por los autores.

CORRESPONDENCIA

dcastroc@unprg.edu.pe

REFERENCIAS

Bibliometrix. (2023). Bibliometrix—Home. https://www.bibliometrix.org/home/index.php

Brookes, B. C. (1985). Bradford’s law and the bibliography of science. In A. Kent (Ed.), Encyclopedia of Library and Information Science (Vol. 15, pp. 95–106). Marcel Dekker.

Chen, L., Chen, P., & Lin, Z. (2020). Artificial Intelligence in Education: A Review. IEEE Access, 8, 75264–75278. https://doi.org/10.1109/ACCESS.2020.2988510

Gao, S., & Jia, R. (2021). Reform of Mathematics Teaching Mode from the Perspective of Artificial Intelligence and Big Data. Lecture Notes on Data Engineering and Communications Technologies, 81, 793–797. https://doi.org/10.1007/978-3-030-79197-1_115

Jin, J., Li, C., & Zhu, Q. (2022). Innovations in AI for Education: Case Studies and Applications. Journal of Educational Technology, 23(5), 78–92. https://doi.org/10.1016/j.edutech.2022.07.003

Kaushik, R., Parmar, M., & Jhamb, S. (2021). Roles and Research Trends of Artificial Intelligence in Mathematics Education. 2021 2nd International Conference on Computational Methods in Science \& Technology (ICCMST), 202–205.

Li, C., & Xing, W. (2022). Revealing Factors Influencing Students’ Perceived Fairness: A Case with a Predictive System for Math Learning. Proceedings of the Ninth ACM Conference on Learning @ Scale, 409–412. https://doi.org/10.1145/3491140.3528293

Li, X., & Zaki, R. (2024). Harnessing the Power of Digital Resources in Mathematics Education: The Potential of Augmented Reality and Artificial Intelligence. EAI/Springer Innovations in Communication and Computing, Part F2195, 191–223. https://doi.org/10.1007/978-3-031-50139-5_10

Lotka, A. J. (1926). The frequency distribution of scientific productivity. Journal of the Washington Academy of Sciences, 16(12), 317–323. https://doi.org/10.5962/bhl.part.29338

McArthur, D., Stasz, C., & Hotta, J. Y. (1987). Learning problem-solving skills in algebra. Journal of Educational Technology Systems, 15(3), 303–324.

Moral-Sánchez, S. N., Rey, F. J. R., & Cebrián-De-la-Serna, M. (2024). Analysis of artificial intelligence chatbots and their potential in education. Computers \& Education.

Müller, J. (2023). Visualizing data with Datawrapper: An introduction to creating interactive charts and maps. Data Visualization Journal, 5(2), 45–60.

Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT press.

Opesemowo, O. A. G., & Adewuyi, H. O. (2024). A systematic review of artificial intelligence in mathematics education: The emergence of 4IR. Eurasia Journal of Mathematics, Science and Technology Education, 20(7), em2478.

Qu, G., Hu, W., Jiao, W., & Jin, J. (2021). Application of deep learning-based integrated trial-error+ science, technology, reading/writing, engineer, arts, mathematics teaching mode in college entrepreneurship education. Frontiers in Psychology, 12, 739362.

Schoenfeld, A. H. (2014). Mathematical problem solving. Elsevier.

Tian, X., Zhao, J., & Nguyen, K. T. (2021). Practical Research on Primary Mathematics Teaching with Artificial Intelligence. Journal of Educational Technology Research and Development.

VOSViewer. (2023). VOSviewer—Visualizing scientific landscapes. https://www.vosviewer.com/