Impacto de la Inteligencia Artificial en el Álgebra Lineal. Una revisión bibliométrica
Impact of Artificial Intelligence on Linear Algebra. A bibliometric review
Carmen Margarita Guzmán Roldán
Universidad Nacional Pedro Ruiz Gallo
Email: cguzmanr@unprg.edu.pe
ORCID: 0000-0002-5073-426X
Miriam María Estrada Huancas
Universidad Nacional Pedro Ruiz Gallo
Email: mestrada@unprg.edu.pe
ORCID: 0000-0002-1628-2685
Rubén Esteban Burga Barboza
Universidad Nacional Pedro Ruiz Gallo
Email: rburga@unprg.edu.pe
ORCID: 0000-0002-1682-5395
Luis Miguel Villegas Santamaría
Universidad Nacional Pedro Ruiz Gallo
Email: lvillegassa@unprg.edu.pe
ORCID: 0000-0001-6535-3884
Recibido : 26/05/2025
Aprobado: 20/08/2025
Publicado : 21/08/2025
Cómo citar este trabajo:
Guzmán Roldán, C.M. et al (2025). Impacto de la Inteligencia Artificial en el Álgebra Lineal: una revisión bibliométrica. Revista Reflexiones De La Sociedad Y Economía, 2(2), 01-24. https://doi.org/10.62776/rse.v2i2.48
![]()
© Los autores. Este artículo es publicado por la Revista Reflexiones de la Sociedad y Economía de la Universidad Nacional Pedro Ruiz Gallo de Lambayeque, Perú, como acceso abierto bajo los términos de la Licencia Creative Commons Atribución 4.0 Internacional (https://creativecommons.org/licenses/by/4.0/. Esta licencia permite compartir (copiar y redistribuir el material en cualquier medio o formato) y adaptar (remezclar, transformar y construir a partir del material) el contenido para cualquier propósito, incluido el uso comercial.
RESUMEN
En el presente artículo se realizó un análisis bibliométrico sobre el impacto de la Inteligencia Artificial (IA) en el Álgebra Lineal, con el objetivo de identificar patrones y tendencias en la producción científica en esta área. Se llevó a cabo una revisión sistemática de la literatura indexada en la base de datos Scopus, aplicando técnicas bibliométricas mediante herramientas especializadas como Bibliometrix y VOSviewer. Se revisaron 779 publicaciones, seleccionando 496 documentos para un análisis detallado, cubriendo un período de 55 años (1969-2024). Desde 2018, las publicaciones han crecido exponencialmente, alineándose con el desarrollo de la IA en la educación superior. Se destacaron los autores más influyentes, como Zhang, Y. y Zhang, S., y las revistas de mayor impacto, incluyendo Lecture Notes in Computer Science. El análisis semántico identificó dos áreas principales de desarrollo: la fundamentación matemática del Álgebra Lineal y su aplicación en redes neuronales y aprendizaje automático. Se observó una baja proporción de colaboraciones internacionales, indicando la necesidad de promover redes de cooperación entre instituciones. El estudio concluyó que la IA facilita la construcción de conocimiento en álgebra lineal al automatizar la extracción de conceptos clave, personalizar el aprendizaje según los datos del estudiante y optimizar el procesamiento algebraico con nuevos algoritmos y hardware, así mismo, las herramientas como ChatGPT hacen las veces de asistentes educativos que median el aprendizaje interactivo, potenciando la comprensión conceptual. En síntesis, la IA transforma tanto la enseñanza como la aplicación del álgebra lo que implica nuevas oportunidades para el desarrollo cognitivo y científico. Se recomienda analizar otras bases de datos e investigar el impacto de la Inteligencia Artificial en la enseñanza del Álgebra Lineal, así como en otras ramas de la matemática mediante estudios empíricos.
Palabras clave: Inteligencia Artificial, Álgebra Lineal, Educación Superior, Revisión Bibliométrica.
ABSTRACT
The present study conducted a bibliometric analysis on the impact of artificial intelligence (AI) in linear algebra, aiming to identify patterns and trends in scientific production within this field. A systematic review of the literature indexed in the Scopus database was carried out, applying bibliometric techniques through specialized tools such as Bibliometrix and VOSviewer. A total of 779 publications were reviewed, with 496 documents selected for detailed analysis, covering a period of 55 years (1969–2024). Since 2018, publications have grown exponentially, aligning with the development of AI in higher education. The most influential authors, such as Zhang, Y. and Zhang, S., as well as the highest-impact journals, including Lecture Notes in Computer Science, were highlighted. Semantic analysis identified two main areas of development: the mathematical foundations of linear algebra and its application in neural networks and machine learning. A low proportion of international collaborations was observed, indicating the need to promote cooperation networks among institutions. The study concluded that AI facilitates the construction of knowledge in linear algebra by automating the extraction of key concepts, personalizing learning according to the student's data and optimizing algebraic processing with new algorithms and hardware. Likewise, tools such as ChatGPT serve as educational assistants that mediate interactive learning, enhancing conceptual understanding. In summary, AI transforms both the teaching and application of algebra, which implies new opportunities for cognitive and scientific development.
It is advisable to examine additional databases and explore the impact of artificial intelligence on the teaching of linear algebra, as well as on other branches of mathematics, through empirical research.
Keywords: Artificial Intelligence, Linear algebra, Higher Education, Bibliometric Review.
INTRODUCCIÓN
En la última década, el avance vertiginoso de la Inteligencia Artificial (IA) ha transformado numerosos campos del conocimiento, desde la medicina y las ciencias sociales hasta las ingenierías y las matemáticas aplicadas. En este contexto, el Álgebra Lineal ha adquirido un rol central al constituirse en la base matemática de múltiples algoritmos de aprendizaje automático, procesamiento de imágenes, sistemas de recomendación y redes neuronales profundas. A nivel global, la articulación entre IA y Álgebra Lineal se ha intensificado no solo en términos de aplicación práctica, sino también en innovación teórica y pedagógica, impulsando desarrollos en hardware, nuevas arquitecturas y plataformas educativas(Kjamilji & Güney, 2023; Li et al., 2021).
En paralelo, avances tecnológicos como la computación en memoria o los sistemas en chip han sido diseñados para optimizar operaciones algebraicas esenciales como la multiplicación de matrices y la descomposición de vectores, fundamentales para las tareas de IA (Feng et al., 2020; Mannocci et al., 2021). Este auge ha motivado a la comunidad científica a explorar cómo los métodos de IA no solo se benefician del Álgebra Lineal, sino también cómo pueden redefinir su enseñanza y eficiencia computacional (Bagno et al., 2024; Margaritis et al., 2023; Zhang, 2024).
Pese a este creciente interés, no se cuenta aún con una visión sistematizada de cómo ha evolucionado la producción científica sobre esta intersección. Esta ausencia dificulta comprender los enfoques predominantes, lagunas de investigación e implicancias señaladas por los autores. Por ello, surge la necesidad de revisar rigurosamente el cuerpo existente de literatura. En este marco, se plantea la siguiente pregunta de investigación: ¿Cuáles son los patrones y tendencias de la producción científica sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal?
Los estudios revisados muestran aplicaciones diversas: enseñanza (Bagno et al., 2024), resolución de problemas complejos (Strahan et al., 2023), eficiencia computacional (Feng et al., 2020), y desarrollo de hardware para tareas algebraicas en IA (Chen et al., 2003; Mannocci et al., 2021; Rende et al., 2024). También se registran experiencias educativas con ChatGPT y modelos generativos en cursos de Álgebra Lineal (Bagno et al., 2024), aunque con limitaciones de validez externa y necesidad de replicación (Nasiri et al., 2017; Zhang, 2024).
Además, varios autores proponen soluciones híbridas para ejecutar con mayor velocidad operaciones algebraicas en contextos de IA (Chen et al., 2003; Peng et al., 2021), aunque advierten una alta dependencia de recursos tecnológicos (Bianchini et al., 2021). Li et al. (2021) y (Kjamilji & Güney, 2023) destacan también la importancia de evaluar la escalabilidad y sostenibilidad de estas soluciones en escenarios con restricciones presupuestales o limitaciones estructurales. Este estudio se justifica por la necesidad de ofrecer una visión panorámica, actualizada y rigurosa de la producción científica sobre IA y Álgebra Lineal. Mediante una revisión bibliométrica, se identifican tendencias, vacíos y oportunidades de investigación interdisciplinaria, ofreciendo una herramienta clave para investigadores, docentes y desarrolladores tecnológicos interesados en este campo emergente.
METODOLOGÍA
Se realizó un análisis bibliométrico el cual tenía como enfoque describir el avance del conocimiento que ha hecho el impacto de la IA en el Álgebra Lineal, con el fin de seguir la metodología establecida por Luna y Luna (2024). Esta metodología incluye diversos pasos sistemáticos, que abarcan la formulación de preguntas de investigación, la selección de bases de datos pertinentes, la elaboración de una ecuación de búsqueda específica y el análisis exhaustivo de los metadatos obtenidos. Es un estudio cuantitativo, de naturaleza exploratoria y descriptiva, de diseño no experimental transeccional. Las preguntas a las propuestas de investigación fueron: ¿Cuáles son los patrones y tendencias de la producción científica sobre el Impacto de la Inteligencia Artificial en el Álgebra Lineal, según un análisis bibliométrico de la literatura existente?, esta pregunta general conlleva a las siguientes interrogantes específicas: a)¿Cuántos estudios se han publicado a lo largo de los años?, b) ¿Quiénes son los autores más activos en el área?, c) ¿Cuáles son las revistas más importantes relacionado con el tema?, d) ¿Cuál es el desarrollo semántico alrededor del fenómeno en estudio?, e) ¿Cuáles son los temas motores en torno al fenómeno en estudio, perspectivas, nichos, temas emergentes?, f) ¿Cuáles son las raíces históricas del concepto o constructo central del tema en estudio?, g) ¿Qué niveles de colaboración han tenido los autores, instituciones y países, etc.?.
Se utilizaron términos clave para construir la ecuación de búsqueda como: TITLE-ABS-KEY (("Artificial Intelligence" OR "Neural Networks" OR "Intelligent Systems" OR "TIC" OR "Educative technology") AND ("LINEAR ALGEBRA")). No se estableció un límite temporal, permitiendo así cubrir el desarrollo del tema desde sus primeros registros en la literatura científica hasta la actualidad. Como resultado de esta búsqueda en la base de datos Scopus, se identificaron 779 publicaciones científicas relevantes.
Los datos obtenidos de Scopus fueron exportados en formato CSV y posteriormente convertidos a Excel para su análisis. Tanto los datos sin procesar como los procesados están disponibles para su visualización en el siguiente enlace: https://drive.google.com/drive/folders/1jgSoX11seiNstT8L0fknitH_pjksEAtA.
Para la generación de las visualizaciones científicas se utilizaron herramientas específicas como Bibliometrix, VosViewer y Datawrapper. Bibliometrix, una herramienta desarrollada en R por el equipo de R Core Team y la R Foundation for Statistical Computing (Bibliometrix, 2024), facilitó el análisis bibliométrico. VOSviewer, un software de código abierto, permitió la creación y visualización de redes bibliométricas (VOSviewer, 2024). Por último, Datawrapper se utilizó para generar gráficos y tablas estadísticas claras y efectivas, esenciales para la comunicación precisa de los resultados en contextos académicos y profesionales.
RESULTADOS
Se presenta la interpretación de cada una de las tablas y figuras obtenidas a partir de la información bibliométrica correspondiente al impacto de la Inteligencia Artificial en el Álgebra Lineal desde que se inician las publicaciones en la base Scopus. Se considera como pregunta central para la investigación ¿Cuáles son los patrones y tendencias de la producción científica sobre el Impacto de la Inteligencia Artificial en el Álgebra Lineal según un análisis bibliométrico de la literatura existente?
En la Tabla 1 se observa que, el análisis bibliométrico sobre el Impacto de la Inteligencia Artificial en el Álgebra Lineal abarcó 55 años (1969-2024), examinando 496 documentos de 779 fuentes distintas. La producción científica no creció anualmente en esos años, con una edad promedio de documentos de 10 años y un promedio de 18 citas por documento. Estos datos reflejan un notable interés en el tema y una significativa influencia de las publicaciones en este campo.
La investigación se distinguió no solo por su extensión, sino también por la notable profundidad alcanzada en el análisis, lo cual se evidencia en la consulta exhaustiva de 22,946 referencias bibliográficas que sustentaron el trabajo. Este esfuerzo se complementó con la utilización de una amplia gama de términos clave, entre los que se contabilizaron 5,164 palabras clave adicionales (Plus) y 1,808 relacionadas directamente con los autores. La riqueza terminológica empleada permitió no solo una identificación más precisa y detallada de la información, sino también una representación fiel de la diversidad de perspectivas, enfoques teóricos y metodológicos presentes en el campo de estudio de la inteligencia artificial.
En este proceso participaron 2,088 autores, cifra que refleja la magnitud de la comunidad académica involucrada en el tema. El promedio de tres coautores por documento revela la importancia de la colaboración y el trabajo conjunto, mientras que la identificación de 111 artículos de autoría individual muestra que aún existe un espacio significativo para los aportes personales y enfoques particulares. Asimismo, resulta relevante destacar que la investigación registró un 17 % de coautorías internacionales, lo cual demuestra no solo el alcance global del interés por la inteligencia artificial, sino también la capacidad de articular conocimientos provenientes de diferentes realidades geográficas, sociales y culturales. Este aspecto enfatiza que el desarrollo científico en torno a la inteligencia artificial no se limita a un contexto local, sino que constituye un fenómeno de carácter mundial, en el cual convergen miradas diversas que enriquecen la comprensión y potencian la construcción de soluciones compartidas.
Tabla 1
Principales indicadores bibliométricos de la colección de metadatos
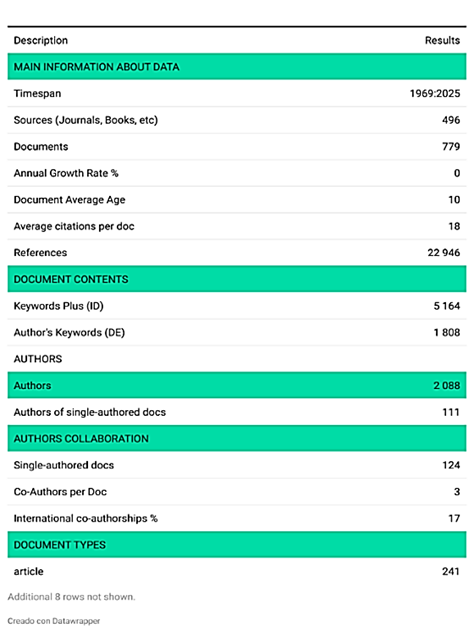
Nota: Data de scopus, procesado en Bibliometrix
A partir de la Figura 1 se dio respuesta a la interrogante ¿Cuál ha sido la evolución de las publicaciones sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal? Se observa que durante los primeros años del período en estudio (1986-2003) se realizaron menos de 15 publicaciones por año relacionados con la Inteligencia Artificial y el Álgebra Lineal, lo cual puede atribuirse a la baja adopción de la Inteligencia Artificial en el ámbito educativo. Sin embargo, desde el 2004 hasta antes del 2018 se nota un incremento moderado en la producción científica, el cual coincide con el avance de la tecnología y un mayor interés en las aplicaciones educativas de la IA. Desde 2018, las publicaciones han aumentado exponencialmente, probablemente debido a la madurez tecnológica, el reconocimiento de la importancia de la IA en la educación y la aceleración de la transformación digital por la pandemia de COVID-19.
Figura 1
Evolución de las publicaciones
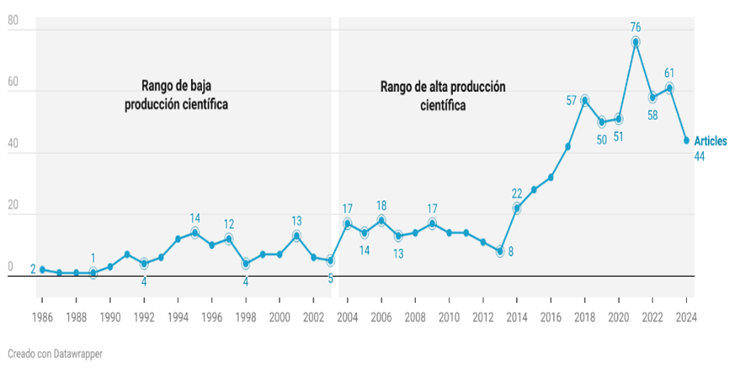
Nota: Nota: Data de scopus, procesado en Bibliometrix
La Tabla 2 fue analizada para dar respuesta a. ¿Quiénes son los autores con mayor actividad sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal? donde se observa que los autores con mayor productividad, impacto y evolución en el área son Zhang, Y. (2009) y Zhang, S. (2015) quienes presentan un alto índice h y una cantidad importante de publicaciones citadas frecuentemente, esto da muestra de un impacto significativo en el área de estudio. En esta misma línea, aunque en menor medida que Zhang, Y. y Zhang, S. tenemos a Ansari, MS. (2009), Boehm, M. (2015), Dongarra, J. (1996), Liu, X. (2017), Mahoney, MW. (2016), Nguyen, HD. (2010), Porello, D. (2010) y Rahman, SA. (2008) que también son relevantes en el tema.
Zhang, Y. (2009) con un total de 11 publicaciones, índice h=6 (6 de sus artículos han sido citados por lo menos 6 veces cada uno), índice g=10 (10 artículos más citados tienen al menos 100 citas en total) e índice m=0.375 (en promedio su índice h ha crecido en 0.375 anualmente desde el 2009 que fue su primera publicación) y un acumulado de 118 citas se posiciona como uno de los autores de mayor influencia en el área de investigación, muestra un alto impacto con un buen equilibrio entre el número de citas y la cantidad de publicaciones. Su índice g sugiere que sus trabajos más citados tienen un fuerte impacto.
Zhang, S. con 8 publicaciones, índice h=5, índice g=8, m=0.5 y 105 citas acumuladas, es otro de los autores, aunque con menos publicaciones que Zhang, Y., tiene un mayor índice m, lo que indica un impacto relativamente fuerte en un corto periodo. Asimismo, Ansari, MS. al haber logrado 8 publicaciones índice h=4, índice g=5 e índice m=0.25 y acumulado 35 citas, tiene un menor número de citas y su índice g refleja que sus publicaciones más citadas tienen un menor impacto en comparación con las de los dos primeros autores.
Mientras que Boehm, M. quien tiene 4 publicaciones, índice h=4, índice g=4 e índice m=0.4 con 226 citas, tiene un alto número de citas en relación a su número de publicaciones, indicando que su trabajo ha sido muy influyente a pesar de su menor número de publicaciones. Dongarra, J. quien ha publicado 6 artículos, índice h=4, índice g=6 e índice m=0.138 y 212 citas, tiene un buen índice g y ha sido prolífico en publicaciones. Sin embargo, su índice m más bajo sugiere que su impacto está más distribuido en el tiempo.
Tabla 2
Principales autores
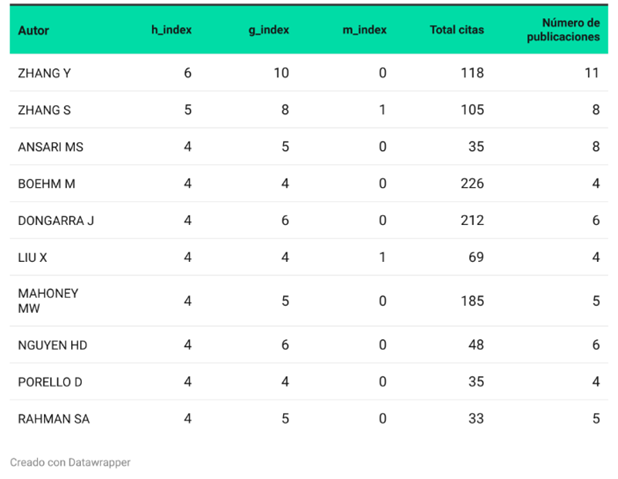
Nota: Data de scopus, procesado en Bibliometrix
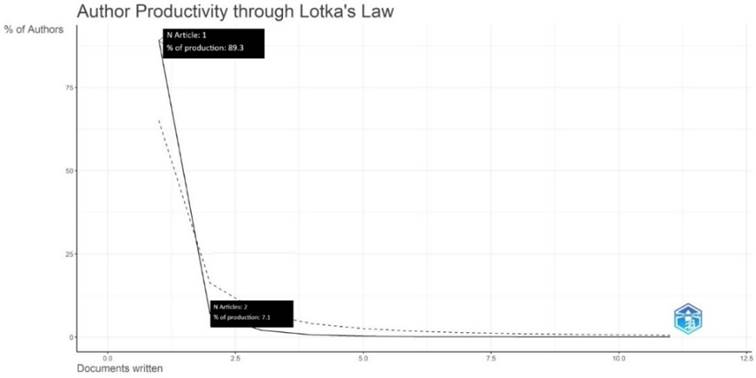
La Tabla 3 y Figura 2 ilustran la aplicación de la Ley de Lotka en un conjunto de datos bibliométricos, lo que permite observar la distribución de la productividad entre los autores.
En la Tabla 3, se observa que la gran mayoría de los autores, el 89.3%, publicaron únicamente un documento, este grupo estuvo compuesto por 1864 autores, lo que confirmó la tendencia generalizada de que la mayoría de los investigadores tienen una producción académica limitada. A medida que aumentó el número de documentos escritos, la cantidad de autores disminuyó drásticamente. Por ejemplo, solo el 7.1% de los autores publicaron dos documentos, mientras que apenas el 2.1% contribuyeron con tres publicaciones. Para los autores que escribieron entre cuatro y ocho documentos, las proporciones fueron insignificantes, con valores que oscilaron entre el 0.7% y 0.1%, lo que reflejó un pequeño grupo de autores altamente productivos.
Tabla 3
Ley de Lotka
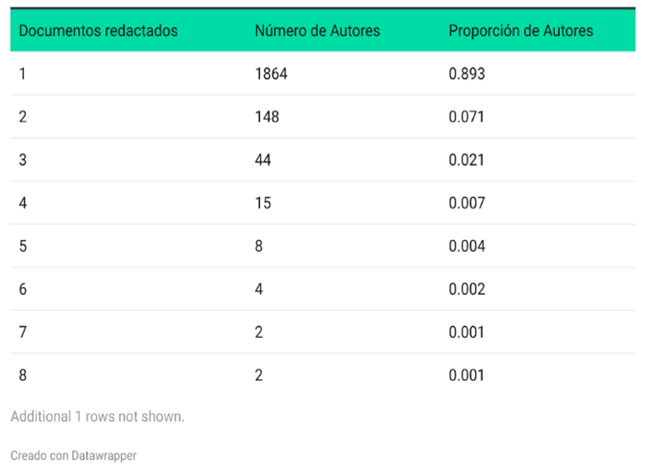
Nota: Data de scopus, procesado en Bibliometrix
En la Figura 2, se representa la gráfica de esta distribución, la curva muestra una caída pronunciada en el porcentaje de autores conforme aumentó el número de documentos escritos, reafirmándose de esta manera lo que señala la Ley de Lotka, de la cual se resalta que un alto porcentaje de la producción (89.3%) provenía de autores que habían escrito un solo artículo, y que solo un 7.1% había producido dos artículos. A medida que se avanzaba hacia autores con mayor número de publicaciones, la curva se estabilizó en un valor muy bajo, lo que indicó que muy pocos autores alcanzaron altos niveles de productividad.
Figura 2
Ley de Lotka
Nota: Data de scopus, procesado en Bibliometrix
En la Tabla 4, se observan las 10 revistas más importantes, según el análisis bibliométrico del tema de investigación. Las revistas señaladas, destacan por las múltiples publicaciones de artículos que abordan temas similares a nuestro fenómeno de estudio.
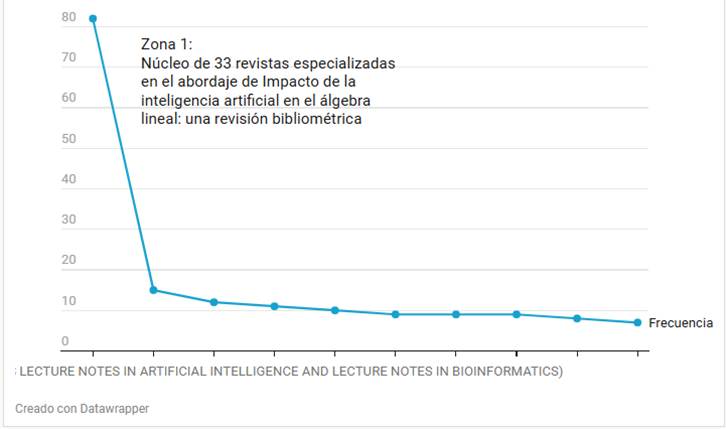
Como punto de partida, de la tabla, se observa que la revista que más ha publicado en los temas de Inteligencia Artificial en el Álgebra Lineal es Lecture Notes in Computer Science presentando una frecuencia de 82, situada muy por debajo, se tiene la revista Proceedings of Spie – The International Society for Optical Engineering con una frecuencia de 15, ACM International Conference Proceeding Series con frecuencia 12, le siguen la revistas Advances in Intelligent Systems and Computing con frecuencia 11, Neurocomputing con una frecuencia de 10, las revistas: IEEE Transactions on Neural Networks, Lecture Notes in Artificial Intelligence y Proceedings of Machine Learning Research con frecuencias de 9, Proceedings of the International Joint Conference on Neural Networks con frecuencia 8 y finalmente la revista IJCAI International Joint Conference on Artificial Intelligence con 7 de frecuencia.
Tabla 4
Principales 10 revistas especializadas (Zona 1 Ley de Bradford)

Nota: Data de scopus, procesado en Bibliometrix
La Figura 3 muestra la aplicación de la Ley de Bradford en un análisis bibliométrico sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal, utilizando Bibliometrix y procesado en Datawrapper. La gráfica presenta una curva decreciente típica de esta ley, donde se observa que un pequeño grupo de revistas concentra la mayor cantidad de publicaciones, mientras que la frecuencia disminuye rápidamente en otras fuentes. En la Zona 1, se identifica un núcleo de 33 revistas especializadas, las cuales contienen la mayor parte de la producción científica sobre el tema en estudio. Esto sugiere que el conocimiento está concentrado en un número reducido de publicaciones clave, mientras que el resto de revistas tienen una menor contribución en términos de frecuencia. Esta distribución es útil para investigadores, ya que permite identificar qué fuentes son más relevantes para consultas bibliográficas.
Figura 3
Ley de Bradford
Nota: Data de scopus, procesado en Bibliometrix
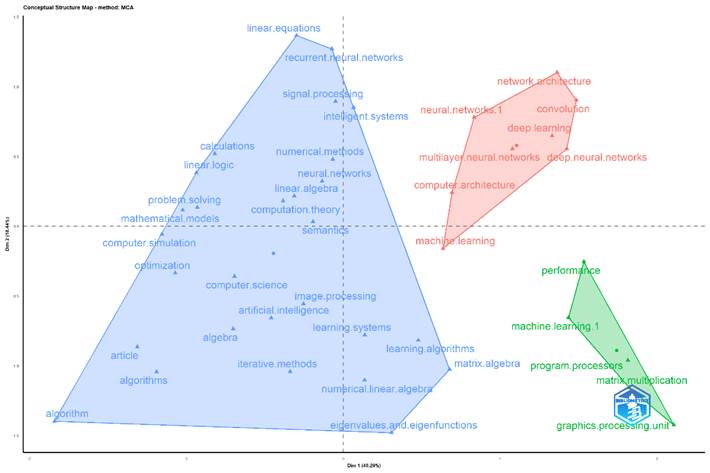
La Figura 4 muestra un Mapa Factorial sobre la relación entre Inteligencia Artificial y Álgebra Lineal, generado mediante un análisis bibliométrico con Bibliometrix. En esta visualización, los conceptos se agrupan en clústeres diferenciados por colores, lo que permite identificar las principales áreas de estudio y sus interconexiones dentro del campo. Se ven tres regiones principales, el clúster azul está relacionado con fundamentos matemáticos, computacionales y algoritmos que van de la mano de conceptos como Álgebra Lineal, ecuaciones lineales, optimización, lógica lineal y redes neuronales. Este grupo muestra que la IA aplicada a las matemáticas se basa en modelos matemáticos y en métodos numéricos esenciales para el procesamiento de información. En segundo lugar, el clúster rojo tiene como foco al aprendizaje profundo, redes neuronales, redes neuronales multicapa, convolución, arquitectura computacional y aprendizaje profundo. En esta región se observa que las técnicas de machine learning avanzadas están conectadas a la matemática, procesamiento y resolución de problemas complejos con redes neuronales. Por último, el clúster verde está relacionado a la ejecución computacional y hardware especializado, los cuales usan terminologías como procesamiento gráfico (GPU), multiplicación (matrices) y optimización del desempeño que muestran que el desarrollo de los modelos depende de gran parte de la optimización del hardware.
Figura 4
Mapa Factorial sobre Inteligencia Artificial y el Álgebra Lineal
Nota: Data de scopus, procesado en Bibliometrix
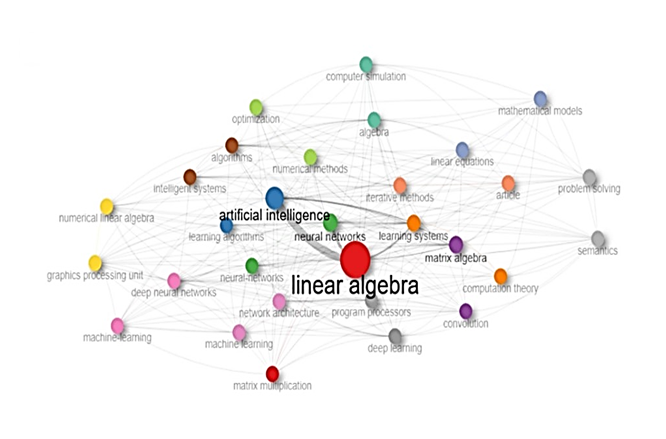
La Figura 5 representa un mapa semántico sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal, generado a partir de datos de Scopus procesados con Bibliometrix. En este gráfico, los términos están organizados en función de su relación y coocurrencia dentro del contexto investigado, donde el tamaño de los nodos indica la relevancia de cada concepto y las conexiones muestran la relación entre ellos.
El término "linear algebra" emerge como el nodo más grande y central, lo cual indica que es un concepto importante a la hora de establecer una relación entre la Inteligencia Artificial y el Álgebra Lineal. Cabe destacar que la gran cantidad de artículos relacionados con términos como "neural networks", "learning systems" y "artificial intelligence" indican que el Álgebra Lineal constituye una disciplina fundamental en la comprensión de los algoritmos de aprendizaje y modelos de Inteligencia Artificial en educación.
Otros términos no muy comunes pero relevantes, son "matrix algebra", "matrix multiplication" y "deep learning", que están directamente relacionados con cálculos fundamentales en redes neuronales y aprendizaje profundo destacando la importancia del cálculo en la optimización y en la manipulación de modelos de la inteligencia artificial. Asimismo, los términos como "optimization", "computer simulation" y "problem solving", están presentes en este mapa, los cuales enfatizan la función de estas técnicas para la solución de problemas matemáticos mediante herramientas computacionales de alta complejidad.
Figura 5
Mapa semántico sobre la Inteligencia Artificial y el Álgebra Lineal
Nota: Data de scopus, procesado en Bibliometrix
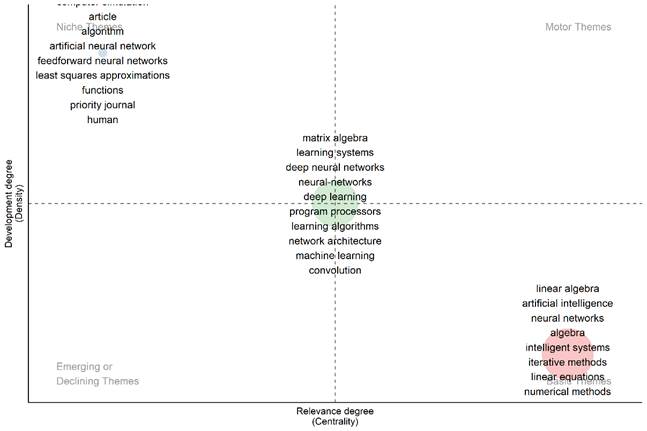
Para responder a la interrogante ¿Cuáles son los temas motores en torno al fenómeno en estudio, perspectivas, nichos, temas emergentes? a partir de la Figura 6, se puede decir que los temas centrales son “matrix algebra”, “learning systems,” “Deep neural networks,” “program processors,” “learning algorithmos,” network architecture, “machien learning” y finalmente convolución.
Los temas básicos se muestran en el cuadrante inferior derecho. Claramente los temas están alineados en dos grupos. El primer grupo está representado por “linear algebra”, “algebra”, “linear equations” referente al desarrollo del tema matemático. El segundo grupo está formando por “artificial inteligence”, “neural networks,” “intelligent systems,” “iterative methods” y “numerical methods” referente a la aplicación del Álgebra Lineal. El cuadrante superior derecho enmarca el grupo de los temas motores, que como se observa no presenta este tipo de temas. Los temas nicho se encuentran en el cuadrante superior izquierdo, los cuales están agrupados en un bloque conformado por “algorithmo,” “artificial neural networks,” “least squares approximations unctions,” “priority journal human”.
El cuadrante inferior izquierdo muestra los temas en declive o emergentes, en el presente estudio no existen estos tipos de temas.
Figura 6
Mapa temático estructural
Nota: Data de scopus, procesado en Bibliometrix
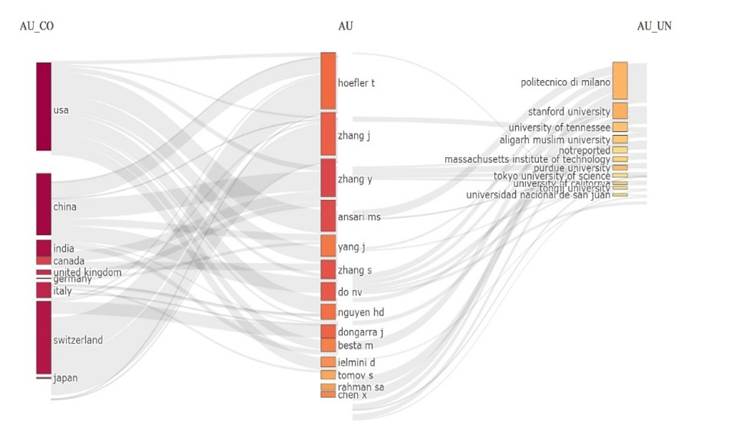
Con el fin de dar respuesta a la pregunta: ¿Qué niveles de colaboración han tenido los autores, instituciones y países, etc.? La Figura 7, El Three-Field Plot, ilustra simultáneamente las relaciones entre el país de afiliación de los autores (AU_CO), los autores más representativos (AU) y las instituciones donde desarrollan su actividad (AU_UN). Los países donde los autores publican con mayor intensidad son Estados Unidos, Suiza y China. Los autores con mayor número de publicaciones, citas, etc son Hoeflet, T, Zhang, J., Zhang, Y., entro otros. Esto nos dice que sus trabajos están muy presentes o colaboran con varias instituciones. Los principales autores están relacionados con las universidades de Tennessee y Purdue. Entre las principales universidades con mayores publicaciones en este rubro se encuentran el Politécnico de Milano, la Universidad de Stanford y la universidad de Tennessee.
Figura 7
Three-Field Plot
Nota: Data de scopus, procesado en Bibliometrix
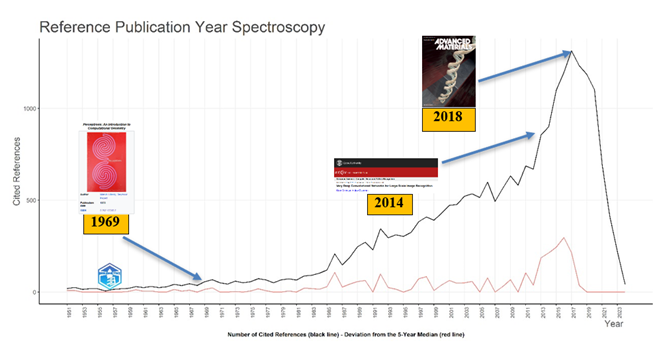
Respecto a la Interrogante ¿Cuáles son las raíces históricas del concepto o constructo central del tema en estudio? La Figura 8 indica que el estudio sobre el “Impacto de la Inteligencia Artificial en el Álgebra Lineal” se inició en el año 1951, en adelante tuvo un crecimiento continuo, destacando su desarrollo los años 1969, 2014 y con un gran auge en el año 2018, debido al gran número de citas.
Mynsky, M; Papert, S. (1969) define el Perceptrons de manera formal como un dispositivo capaz de calcular todos los predicados que son lineales en un conjunto dado de predicados
parciales. El trabajo está dividido en unidades: en la primera se presenta la teoría algebraica necesaria para el desarrollo del tema, en la segunda parte se estudia las propiedades geométricas del Perceptrons, para ello estudia cierta función Yconexa, en la tercera parte, se estudia la teoría del aprendizaje. De las representaciones lineales se estudian sus coeficientes y se cuestiona cómo calcular estos coeficientes y que tan eficientes son para almacenar información, el trabajo demuestra que estos coeficientes crecen más rápido que de manera exponencial. En el capítulo 11 se estudia el teorema de convergencia de Perceptrón relacionándolos con fenómenos familiares asociados con las máquinas de estados finitos, con la teoría de la optimización y con la retroalimentación como dispositivo computacional. El Capítulo 12 el autor deja de lado la definición estricta del Perceptrón para estudiar una familia más grande de ciertos algoritmos que converge más rápido que de manera exponencial.
Simonyan & Andrew Zisserman (2014) investigan sobre el efecto de la profundidad de la red convolucional en su precisión en el contexto del reconocimiento de imágenes a gran escala. La principal contribución fue una evaluación exhaustiva de redes de profundidad creciente utilizando una arquitectura con ciertos filtros de convolución muy pequeños (3×3). Se muestras que estos cambios en la profundidad proporcionan mejoras significativas en la técnica anterior, aquí también se demuestra que estos métodos se pueden aplicar a otros conjuntos de datos.
Hu, M. et al (2018) en su trabajo “Memristor-Based Analog Computation and Neural Network Classification with a Dot Product Engine” indican que aplicar matrices de barras cruzadas de memristores globales para acelerar los cálculos computacionales es un nuevo modo en la implementación de algoritmos para redes neuronales profundas. Sin embargo, las primeras aplicaciones, por los desafíos propios de la materiales y dispositivos, se han limitado a franjas de simulaciones o aplicaciones de pequeña escala, ya que las matrices grandes con valores estables y analógicos no son programables, su investigación está enfocada en superar estos inconvenientes, obteniendo una precisión analógica alta y ajuste de alta precisión en celdas de memristores concatenados en una matriz de 128×64. En este trabajo también se evalúa la precisión en multiplicación de matrices vectoriales.
Figura 8
Espectroscopía del año de la referencia citada (raíces históricas del tema)
Nota: Data de scopus, procesado en Bibliometrix
DISCUSIÓN
Los resultados de la presente investigación, consecuencia de la observación de la historia de producción científica sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal, coinciden con estudios previos en el ámbito de las ciencias de la computación y la educación. La Figura 1 muestra un crecimiento exponencial de las publicaciones desde 2018, período en que la tecnología se desarrolló de un modo vertiginoso y se aceleró la digitalización por la pandemia de COVID-19. Este hallazgo se alinea con la investigación de Bagno et al. (2024), quienes destacan la incorporación de ChatGPT en la enseñanza del Álgebra Lineal como una innovación clave en los últimos años, quienes también enfatizan la necesidad de evaluar los efectos pedagógicos de estas herramientas, sin embrago el presente estudio revela un interés creciente en la incorporación de la IA en el álgebra lineal.
En cuanto a los principales autores en la investigación del impacto de la Inteligencia Artificial en el Álgebra Lineal (Tabla 2), se identificaron a Zhang, Y. (2009) y Zhang, S. (2015) como los más influyentes. Esta tendencia es consistente con trabajos recientes como el de Zhang (2024), quien exploró métodos innovadores en la enseñanza del Álgebra Lineal con IA. Sin embargo, a diferencia de los hallazgos obtenidos en la presente investigación, el estudio de Zhang enfatiza estrategias específicas de aplicación en el aula, mientras que este estudio bibliométrico se centra en la producción académica en general.
El análisis de las principales revistas (Tabla 4) revela que Lecture Notes in Computer Science es la publicación con mayor frecuencia de artículos sobre el tema. Esto coincide con estudios anteriores, como el de Strahan et al. (2023), quienes llevaron a cabo métodos iterativos en
Álgebra Lineal y observaron un buen respaldo de estos cursos en revistas de computación. No obstante, mientras que el presente estudio destaca la concentración de publicaciones en ciertas revistas, Strahan et al. (2023) sugieren una mayor diversificación de fuentes en el futuro.
El mapa temático estructural (Figura 6) muestra que "matrix algebra" y "learning systems" son los temas motores del campo. Este resultado concuerda con el estudio de Mannocci et al. (2021), quienes estudiaron el uso de arquitecturas computacionales en cálculo matricial, acotando la importancia del Álgebra Lineal en la optimización de los modelos IA. Sin embargo, los resultados obtenidos, revelan una división clara entre los temas matemáticos y las aplicaciones en IA, mientras que Mannocci et al. (2021) argumentan que estos elementos están cada vez más interconectados.
La espectroscopía del año de la referencia citada (Figura 8) muestra que las raíces históricas del impacto de la Inteligencia Artificial en el Álgebra Lineal se remontan a 1951, con hitos clave en 1969, 2014 y 2018. Esto corresponde al artículo de Cherkassky et al. (1991), quienes usaron un enfoque algebraico para modelos neuronales, que muestra la evolución de la materia. Sin embargo, a diferencia de hallazgos obtenidos, en el presente estudio, Cherkassky et al. (1991) no predijeron el impacto que la IA tendría en la educación superior en las décadas siguientes.
El estudio realiza un análisis minucioso sobre la evolución bibliométrica de la Inteligencia Artificial en el Álgebra Lineal, ofreciendo un marco para futuras investigaciones. Se reconocieron patrones de evolución, autores influyentes, revistas relevantes, temas de actualidad lo que permite la comprensión sobre el origen y evolución de este campo de estudio y sus futuras perspectivas.
Una limitación de este estudio es el uso exclusivo de la base de datos Scopus, lo que podría generar un sesgo al excluir publicaciones relevantes en otras bases como Web of Science o IEEE Xplore. También el análisis está basado en metadatos, por lo que no es posible una evaluación de fondo del contenido de los artículos analizados.
Para futuras investigaciones, se recomienda ampliar el análisis a otras bases de datos y examinar el impacto de la Inteligencia Artificial en la enseñanza del Álgebra Lineal, así como en otras ramas de la matemática mediante estudios empíricos. El estudio del impacto de nuevas tecnologías como modelo de lenguaje generativo podría ofrecer una visión más integral sobre el impacto de la IA en este ámbito académico.
CONCLUSIONES
El estudio bibliométrico sobre el impacto de la Inteligencia Artificial en el Álgebra Lineal permitió identificar algunos patrones relevantes en la producción científica, ofreciendo una imagen general del área de desarrollo y de tendencias en la investigación referida, para esta área. Se evidenció que, a pesar de que la literatura académica en este campo abarca más de cinco décadas, el crecimiento de las publicaciones ha sido exponencial en los últimos años, especialmente desde 2018. Este incremento coincide con la madurez de la Inteligencia Artificial y su aplicación en la educación, impulsado en parte por la digitalización acelerada de los procesos educativos.
En cuanto a los autores más influyentes, se identificó un grupo reducido de investigadores con una alta producción y un impacto significativo en el campo, destacando Zhang, Y. y Zhang, S., cuyas publicaciones han recibido un considerable número de citas. Así mismo la Ley de Lotka señala, en este estudio, que la mayoría de los investigadores habían escrito un solo artículo, manifestando el fenómeno de la dispersión del conocimiento de la que solo ha producido un pequeño número de autores alcanzando un perfil de producción estable. Este hallazgo resalta la necesidad de fortalecer la colaboración entre investigadores para consolidar un cuerpo de conocimiento más estructurado y cohesionado.
En lo que respecta a las fuentes de publicación, la concentración de artículos en revistas especializadas como Lecture Notes in Computer Science y Proceedings of SPIE sugiere que el campo está dominado por publicaciones de alto impacto en computación e inteligencia artificial. La dispersión según la Ley de Bradford mostró que un pequeño núcleo de revistas está fuera de las que comprenden la mayor parte de la producción científica logrando así identificar las fuentes de donde se pueden obtener investigaciones futuras. No obstante, se observa una necesidad de diversificación de publicaciones en otras revistas multidisciplinarias para fomentar la difusión del conocimiento a audiencias más amplias.
El análisis semántico y temático permitió establecer que el desarrollo conceptual del campo se organiza en torno a dos grandes áreas: la fundamentación matemática del Álgebra Lineal y su aplicación en redes neuronales y aprendizaje automático. Los términos como matrix algebra, learning systems y deep neural networks emergen como temas motores, indicando que la Inteligencia Artificial ha potenciado la aplicabilidad del Álgebra Lineal en la optimización de modelos computacionales. También, el estudio de las raíces históricas demostró que este campo ha evolucionado en consecuencia de avances críticos en teoría del perceptrón y aprendizaje profundo, puntos importantes sobre la investigación de las redes neuronales.
En términos de colaboración, el análisis bibliométrico mostró que la investigación está liderada por instituciones de alto prestigio como la Universidad de Tennessee y el Politécnico de Milano, con un predominio de publicaciones provenientes de Estados Unidos, Suiza y China. Por otro lado, la cifra escasa de coautorías internacionales muestra la necesidad de estimular redes de intercambio, en efecto, entre instituciones de diversos estados para la colaboración con distintas perspectivas de estudio para enriquecer y conseguir la integración de diferentes enfoques.
A partir del análisis bibliométrico realizado, se concluye que la Inteligencia Artificial ha comenzado a desempeñar un papel clave en el aprendizaje y la enseñanza del Álgebra Lineal. Esta tecnología permite extraer conceptos esenciales de forma automatizada, adaptar los contenidos al ritmo y necesidades del estudiante, y mejorar el procesamiento algebraico mediante algoritmos avanzados y nuevos entornos computacionales. Herramientas como ChatGPT actúan como mediadores del aprendizaje, promoviendo una comprensión más profunda e interactiva. Además, el estudio evidencia un interés creciente en la comunidad científica por integrar la IA en este campo, lo cual abre nuevas posibilidades para fortalecer el desarrollo cognitivo y la formación académica desde un enfoque más personalizado e innovador.
APORTES DE LOS AUTORES
Carmen Margarita Guzmán Roldán: Conceptualización, investigación, visualización, redacción borrador original, administración de Proyecto.
Miriam María Estrada Huancas: Conceptualización, investigación, visualización, redacción borrador original, curación de datos.
Rubén Esteban Burga Barboza: Conceptualización, investigación, visualización, redacción borrador original.
Luis Miguel Villegas Santamaría: Conceptualización, investigación, visualización, redacción borrador original, Software.
Los autores declaran que no existen conflictos de intereses que puedan haber influido en la realización de esta investigación, el análisis de los resultados o la redacción del presente manuscrito.
RESPONSABILIDAD ÉTICA Y LEGAL
Este estudio se llevó a cabo respetando el código de ética de la American Psychological Association (APA 7ma edición). Se trabajó con documentos de archivo y fuentes secundarias, asegurando un manejo ético de la información, el respeto a los derechos de autor, y la adecuada citación de los materiales utilizados. Se ha garantizado que la interpretación de los datos históricos se realiza con rigurosidad y responsabilidad, sin distorsionar el contexto original.
DECLARACIÓN SOBRE EL USO DE INTELIGENCIA ARTIFICIAL - LLM
En esta investigación se utilizó el modelo de lenguaje extenso ChatGPT-4 para apoyar la redacción de secciones preliminares del manuscrito y para mejorar la redacción de los textos. Sin embargo, toda la interpretación de resultados, redacción final y conclusiones fueron revisadas y validadas por los autores, quienes asumen la plena responsabilidad sobre el contenido presentado. Los autores son responsables de la veracidad, integridad y precisión de los datos y argumentos presentados. Se reconoce que los modelos de lenguaje pueden contener sesgos o limitaciones inherentes, por lo que todo el contenido fue revisado para asegurar su adecuación a los estándares académicos.
FINANCIAMIENTO
Este estudio fue financiado íntegramente por los autores.
CORRESPONDENCIA
REFERENCIAS
Bagno, E., Dana-Picard, T., & Reches, S. (2024). ChatGPT in Teaching Linear Algebra: Strides Forward, Steps to Go. Open Education Studies, 6(1). Scopus. https://doi.org/10.1515/edu-2024-0031
Bianchini, B., de Lima, G., & Gomes, E. (2021). Linear algebra in engineering: An analysis of Latin American studies. ZDM - Mathematics Education, 51(7), 1097-1110. Scopus. https://doi.org/10.1007/s11858-019-01081-5
Bibliometrix. (2024). Bibliometrix-Home. https://www.bibliometrix.org/home/
Chen, Z., Dongarra, J., Luszczek, P., & Roche, K. (2003). Self-adapting software for numerical linear algebra library routines on clusters. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2659, 665-672. Scopus. https://doi.org/10.1007/3-540-44863-2_65
Cherkassky, V., Fassett, K., & Vassilas, N. (1991). Linear Algebra Approach to Neural Associative Memories and Noise Performance of Neural Classifiers. IEEE Transactions on Computers, 40(12), 1429-1435. Scopus. https://doi.org/10.1109/12.106229
Feng, K., Kong, T., Koul, K., Melchert, J., Carsello, A., Liu, Q., Nyengele, G., Strange, M., Zhang, K., Nayak, A., Setter, J., Thomas, J., Sreedhar, K., Chen, P., Bhagdikar, N., Myers, Z. A., D’Agostino, B., Joshi, P., Richardson, S., … Raina, P. (2020). Amber: A 16-nm System-on-Chip With a Coarse- Grained Reconfigurable Array for Flexible Acceleration of Dense Linear Algebra. IEEE Journal of Solid-State Circuits, 59(3), 947-959. Scopus. https://doi.org/10.1109/JSSC.2023.3313116
Kjamilji, A., & Güney, O. (2023). Highly efficient secure linear algebra for private machine learning classifications over malicious clients in the post-quantum world. Journal of King Saud University - Computer and Information Sciences, 35(9). Scopus. https://doi.org/10.1016/j.jksuci.2023.101718
Li, F., Ye, Y., Tian, Z., & Zhang, X. (2021). CPU versus GPU: which can perform matrix computation faster—Performance comparison for basic linear algebra subprograms.
Neural Computing and Applications, 31(8), 4353-4365. Scopus. https://doi.org/10.1007/s00521-018-3354-z
Luna, M., & Luna, E. (2024). La biblioteca y el bibliotecario: El punto de vista de los usuarios de centros CONAHCYT. Biblioteca Universitaria, 26(2), Article 2. https://doi.org/10.22201/dgbsdi.0187750xp.2023.2.1512
Mannocci, P., Pedretti, G., Giannone, E., Melacarne, E., Sun, Z., & Ielmini, D. (2021). A Universal, Analog, In-Memory Computing Primitive for Linear Algebra Using Memristors. IEEE Transactions on Circuits and Systems I: Regular Papers, 68(12), 4889-4899. Scopus. https://doi.org/10.1109/TCSI.2021.3122278
Margaritis, K., Adamopoulos, M., Goulianas, K., & Evans, D. (2023). Artificial neural networks and iterative linear algebra methods. Parallel Algorithms and Applications, 3(1-2), 31-44. Scopus. https://doi.org/10.1080/10637199408962524
Nasiri, M., Minaei, B., & Sharifi, Z. (2017). Adjusting data sparsity problem using linear algebra and machine learning algorithm. Applied Soft Computing Journal, 61, 1153-1159. Scopus. https://doi.org/10.1016/j.asoc.2017.05.042
Peng, C., Chen, W., & Wei, A. (2021). Teaching capm for a pre-finance graduate program at the stem undergraduate level: Linear algebra perspective. Mathematics, 9(14). Scopus. https://doi.org/10.3390/math9141668
Rende, R., Viteritti, L., Bardone, L., Becca, F., & Goldt, S. (2024). A simple linear algebra identity to optimize large-scale neural network quantum states. Communications Physics, 7(1). Scopus. https://doi.org/10.1038/s42005-024-01732-4
Strahan, J., Guo, S., Lorpaiboon, C., Dinner, A., & Weare, J. (2023). Inexact iterative numerical linear algebra for neural network-based spectral estimation and rare-event prediction. Journal of Chemical Physics, 159(1). Scopus. https://doi.org/10.1063/5.0151309
VOSviewer. (2024). VOSviewer-Visualizing scientific landscapes. VOSviewer. https://www.vosviewer.com//
Zhang, J. (2024). Exploration of Innovative Teaching Methods in the Teaching Reform of Linear Algebra Course in the Internet Era. Applied Mathematics and Nonlinear Sciences, 9(1). Scopus. https://doi.org/10.2478/amns-2024-0278